Uma barra de aço de espessura Ah, para ser usada como viga, é soldada a um suporte vertical por dois filetes de solda conforme mostrado na figura.
(a) Encontre a força F de flexão segura se a tensão de cisalhamento admissível nas soldas é \tau_{adm} .
(b) Na parte a, você encontra uma expressão simples para F em termos da tensão de cisalhamento admissível.
Encontre a carga admissível se o eletrodo é o E7010, a barra é de aço 1020 laminado a quente, e o suporte é de aço 1015 laminado a quente.
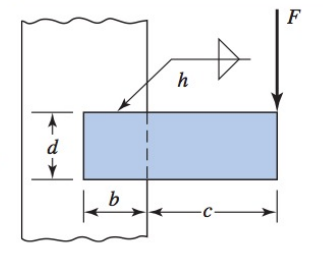
Dados do problema: b = d = 50 mm ; c = 150 mm; h = 5 mm ; \tau_{adm} = 140 MPa ;
(a)
Cisalhamento primário:
Iremos utilizar a área dada na tabela 9-1, para o caso 2
\tau'_{y} = \dfrac{V}{A} = \dfrac{F*10^3}{1,414*5*50} = 2,829 F
Cisalhamento secundário:
J_{u} = \dfrac{d(3b^2 + d^2)}{6} = \dfrac{50[3*50^2+50^2]}{6} = 83,33*10^3 mm^3
J = 0,707h J_u = 0,707*5*8333*10^3 = 294,6*10^3 mm^4
J = 0,707h J_u = 0,707*5*8333*10^3 = 294,6*10^3 mm^4
\tau''_{x} = \tau''_{y} = \dfrac{Mr}{J} = \dfrac{175*F*10^3*25}{294,6*10^3} = 14,85F
\tau_{\max }=\sqrt{\tau_x^{\prime \prime 2}+\left(\tau_y^{\prime}+\tau_y^{\prime \prime}\right)^2}=F \sqrt{14,85^2+(2,829+14,85)^2}=23,1 F
F = \dfrac{\tau_{adm}}{23,1} = \dfrac{140}{23,1} = 6,06 kN
(b)
Para o E7010, da tabela 9-6, \tau'_{y} = \dfrac{V}{A} = \dfrac{F*10^3}{1,414*5*50} = 2,829 F
Encontrando as resistências do suporte e barra:
1020 HR : S_{ut} = 380 MPa , S_{y} = 210 MPa
1015 HR: S_{ut} = 340 MPa , S_{y} = 190 MPa
Da tabela 9-3, do eletrodo E7010 : S_{ut} = 482 MPa , S_{y} = 393 MPa
Iremos partir do suporte, já que este tem menor resistência
primeiro, vamos olhar na tabela 9-4 o tipo de carregamento para assim encontrar a tensão admissível. Como o carregamento é cisalhante, temos que
\tau_{adm} = min(0,30S_{ut};0,40S_{y})
\tau_{adm} = min(0,30*340;0,40*190)
\tau_{adm} = min(102;76) = \tau_{adm} = 76 MPa
Da tensão admissível, a força será
F = \dfrac{\tau_{adm}}{23,1} = \dfrac{76}{23,1} = 3,29 kN

