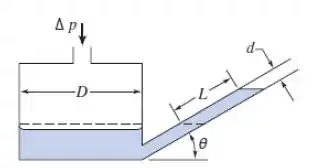
O manômetro de tubo inclinado mostrado tem D = 96 mm e d = 8 mm. Determine o ângulo, \theta, necessário para fornecer um aumento de 5:1 na deflexão do líquido, L, comparada com a deflexão total de um manômetro comum de tubo em U. Avalie a sensibilidade do manômetro de tubo inclinado.
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que:
\dfrac{d p}{d z}=-\rho g
Integrando a pressão hidrostática, ficamos com:
\Delta \rho=-\rho g \Delta z
Aplicando a equação do ponto 1 até o 2 :
p_1-\rho g(x+\operatorname{Len}(\theta))=p_2
Simplificando e manipulando a equação acima:
p_1-p_2=\rho g(x+L \operatorname{sen}(\theta))
Como o volume permanece constante:
\dfrac{\pi}{4} D^2 x=\dfrac{\pi}{4} d^2 L
x=\left(\dfrac{d}{D}\right)^2 L
Logo:
p_1-p_2=\rho g L\left[\left(\dfrac{d}{D}\right)^2+\operatorname{sen}(\theta)\right]
Agora para um tubo em U:
p_1-p_2=\rho g h
Logo:
\dfrac{p_1-p_2}{p_{U 1}-P_{U 2}}=\dfrac{\rho g L\left[\left(\dfrac{d}{D}\right)^2+\operatorname{sen}(\theta)\right]}{\rho g h}
Para pressões aplicadas iguais:
\mathrm{L}\left[\left(\dfrac{d}{D}\right)^2+\operatorname{sen}(\theta)\right]=h
No entanto, sabemos que $\frac{L}{h}=5$, logo, substituindo e isolando o ângulo:
\theta=11,13^{\circ}
A sensibilidade do manômetro, por sua vez, será:
s=\dfrac{L}{\Delta h_e}=\dfrac{L}{S G h}
De novo, como \dfrac{L}{h}=5:
s=\dfrac{5}{S G}
Resposta
\theta=11,13^{\circ}
s=\dfrac{5}{S G}

