Com uma explicação não tão sofisticada quanto as que encontramos no livro do Tocci, tentarei definir as operações com portas OR e AND.
PORTA OR
Uma das melhores maneiras de enxergar seu funcionamento é através da expressão booleana que a representa:
x=A+B
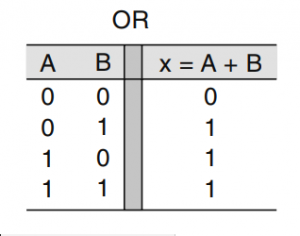
Lemos essa expressão como “x é igual a A ou B”. Nessa expressão o “+” não representa a adição matemática, ela representa o “OR”. Nessa porta, basta uma entrada ser alta (nível lógico 1) para que sua saída seja alta. A única maneira de não haver saída alta é com as duas entradas em nível baixo (nível lógico 0). Vejamos a tabela verdade que define a operação OR:
Figura 1: Tabela-verdade da operação OR.
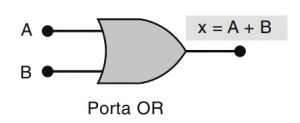
Dentro de um circuito ou de um CI, a representação dessa porta é da seguinte maneira:
Figura 2: Símbolo de uma porta OR.
PORTA AND
Diferentemente da porta OR, a AND precisa necessariamente que todas suas portas sejam altas para que sua saída seja alta, sua equação booleana fica da seguinte maneira:
x=A.B
Lemos essa expressão como “x é igual a A e B”. Sendo o “AND” representado pela multiplicação. Abaixo sua tabela verdade:
Figura 3: Tabela-verdade da operação AND
Dentro de um circuito ou de um CI, a representação dessa porta é da seguinte maneira:
Figura 4: Símbolo de uma porta AND
Vale ressaltar que a representação usada aqui usa apenas duas entras nas portas, porém, podemos encontras portas com mais entradas e, consequentemente, uma tabela-verdade de acordo.
Inscrever-se
0 Comentários
mais antigos