O primeiro volume do livro de Física do Halliday trata da parte Mecânica. Nesta postagem trarei exercícios resolvidos do Capítulo 2 (Movimento Retilíneo) da 10ª edição.
Exercícios resolvidos: 32/119 – Atualizado 18/06/22
DICA: Use o Ctr+F (pesquisar) para encontrar a questão que você deseja.
1) Se você está dirigindo um carro a 90 km/h, e seus olhos permanecem fechados por 0,50 s por causa de um espirro, qual é a distância percorrida pelo carro até você abrir novamente os olhos?
Dados:
V = 90 km/h = 25 m/s
t = 0,50 s
Aplicando:
D = V×t
D = 25×0,50
D = 12,5 m
2) Calcule sua velocidade média nos dois casos seguintes: (a) você caminha 73,2 m a uma velocidade de 1,22 m/s e depois corre 73,2 m a uma velocidade de 3,05 m/s em uma pista reta; (b) você caminha 1,00 min a uma velocidade de 1,22 m/s e depois corre por 1,00 min a 3,05 m/s em uma pista reta. (c) Faça o gráfico de x em função de t nos dois casos e indique de que forma a velocidade média pode ser
determinada a partir do gráfico.
a) Usando o fato de que tempo = distância / velocidade enquanto a velocidade é constante, nós
encontramos

b) Usando o fato de que a distância = vt enquanto a velocidade v é constante, encontramos
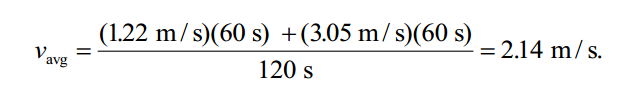
(c) Os gráficos são mostrados abaixo (com metros e segundos compreendidos). O primeiro
consiste em dois segmentos de linha (sólidos), o primeiro tendo um declive de 1,22 e o segundo
tendo uma inclinação de 3,05. A inclinação da linha tracejada representa a velocidade média (em
ambos os gráficos). O segundo gráfico também consiste em dois segmentos de linha (sólidos), tendo
mesmo declive como antes – a principal diferença (comparado ao primeiro gráfico) é que
o estágio que envolve movimentos de alta velocidade dura muito mais tempo.

3) Um automóvel viaja em uma estrada retilínea por 40 km a 30 km/h. Em seguida, continuando no mesmo sentido, percorre outros 40 km a 60 km/h. (a) Qual é a velocidade média do carro durante esse percurso de 80 km? (Suponha que o carro está se movendo no sentido positivo do eixo x.) (b) Qual é a velocidade escalar média? (c) Desenhe o gráfico de x em função de t e mostre como calcular a velocidade média a partir do gráfico.
Sabemos do enunciado que:
Trajeto I:
- d = 40 km
- v = 30 km/h
Trajeto II:
- d = 40 km
- v = 60 km/h
(a)
A velocidade media é dada pela razão entre o distância total percorrida em um intervalo de tempo total (∆t) Sabendo que foram percorridos 80 km no total, em intervalos de tempos diferentes:
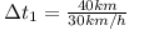


Assim a velocidade media é:
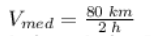
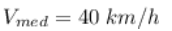
(b)
Da mesma forma, a velocidade escalar media é dada pela razão entre o distância total percorrida em um intervalo de tempo total (∆t), por tabto ela é:
(c)
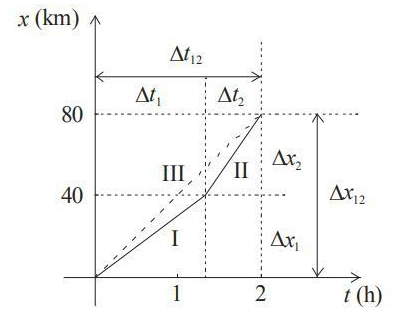
- A linha I representa o primeiro trajeto da viagem
- A linha II representa o segundo trajeto da viagem .
- A linha III representa ao trajeto total
Assim a velocidade média de cada trajeto é dada pelos declives das linhas.
4) Um carro sobe uma ladeira a uma velocidade constante de 40 km/h e desce a ladeira a uma velocidade constante de 60 km/h. Calcule a velocidade escalar média durante a viagem de ida e volta.
Vamos chamar de x a distancia que ele percorre ao subir descer a ladeira, então vamos encontrar o tempo.
Na subida
V = x/t
t = x/40
Na descida
V = x/t
t = x/60
O espaço total percorrido X = x + x = 2x
O tempo total
T = x/40 + x/60 MMC de 40 e 60 = 120
T = 3x + 2x/120
T = 5x/120
T = x/24
Tempo total x/24
Espaço total 2x
velocidade media
V = 2x/x24 divisão de fração por fração
V = 2x.24/x
V = 48km/h
5) A posição de um objeto que se move ao longo de um eixo x é dada por x = 3t − 4t, em que x está
em metros e t em segundos. Determine a posição do objeto para os seguintes valores de t: (a) 1 s, (b) 2 s, (c) 3 s, (d) 4 s. (e) Qual é o deslocamento do objeto entre t = 0 e t = 4 s? (f) Qual é a velocidade média no intervalo de tempo de t = 2 s a t = 4 s? (g) Desenhe o gráfico de x em função de t para 0 ≤ t ≤ 4 s e indique como a resposta do item (f) pode ser determinada a partir do gráfico.
Para os valores de t basta substitui-los na equação:
a) x=3(1)-4(1)²+1³ = 0
b) x=3(2)-4(2)²+2³ = -2
c) x=3(3)-4(3)²+3³= 0
d) x=3(4)-4(4)²+4³=12
(e) A posição em t=0 é x=0. Assim, o deslocamento entre t=0 e t=4 s é:
Δ = x (4s) – x (0) = 12 – 0 = 12 m
f) v= d / t
v= 14/2 → v= 7m/s
6) Em 1992, o recorde mundial de velocidade em bicicleta foi estabelecido por Chris Huber. O tempo
para percorrer um trecho de 200 m foi de apenas 6,509 s, o que motivou o seguinte comentário de Chris: “Cogito ergo zoom!” (Penso, logo corro!). Em 2001, Sam Whittingham quebrou o recorde de Huber por 19 km/h. Qual foi o tempo gasto por Whittingham para percorrer os 200 m?
Podemos afirmar que o tempo gasto por Sam Whittingham nos 200m foi o equivalente a 5,554 segundos.
Para responder essa questão, primeiro você deve observar a velocidade média estabelecida por Chris Huber, acompanhe o raciocínio:
–> divida o espaço pelo tempo-
200/6,509
Assim, diremos que a velocidade média praticada por Chris Huber equivale a 30.726 metros/segundo.
–> o próximo passo é transformar a velocidade de metros/segundo em Km/h, fazendo a multiplicação daquele valor por 3,6:
30.726 * 3,6
Vm= 110,613 Km/h
–> Sam quebrou o recorde dele em 19 Km/h
com isso, basta que você some 110,613 Km/h + 19 Km/Hh
o que resulta em 129,613 Km/Hh
–> Agora precisamos da velocidade de Sam dada em m/s:
129,613 / 3,6 = 36,004 m/s.
200 / 36,004 =
5,554 Segundos
7) Dois trens, ambos se movendo a uma velocidade de 30 km/h, trafegam em sentidos opostos na mesma linha férrea retilínea. Um pássaro parte da extremidade dianteira de um dos trens, quando estão separados por 60 km, voando a 60 km/h, e se dirige em linha reta para o outro trem. Quando chegar ao outro trem, o pássaro faz meia-volta e se dirige para o primeiro trem, e assim por diante. Qual é a distância que o pássaro percorre até os trens colidirem?
O pássaro percorre uma distância de 60 km.
As equações de posição dos dois trens são (t dado em horas):
Sa = 30t
Sb = 60 – 30t
Sendo assim, os trens irão se colidir no instante:
30t = 60 – 30t
60t = 60
t = 1 h
Ou seja, depois de uma hora, os trens irão se colidir. Como o pássaro voa a 60 km/h desde o momento inicial até a colisão dos trens, ele voa então por uma hora, totalizando 60 km percorridos.
8) Situação de pânico. A Fig. 2-24 mostra uma situação na qual muitas pessoas tentam escapar
por uma porta de emergência que está trancada. As pessoas se aproximam da porta a uma velocidade vs=3,50 m/s, têm d = 0,25 m de espessura e estão separadas por uma distância L = 1,75 m. A Fig. 2-24
mostra a posição das pessoas no instante t = 0. (a) Qual é a taxa média de aumento da camada de pessoas que se comprimem contra a porta? (b) Em que instante a espessura da camada chega a 5,0 m? (As respostas mostram com que rapidez uma situação desse tipo pode colocar em risco a vida das pessoas.)
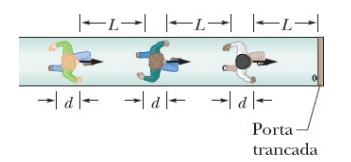
A quantidade de tempo que leva para cada pessoa mover uma distância L com velocidade Vs é
Δt = L / Vs. Com cada pessoa adicional, a profundidade aumenta em uma profundidade de corpo d
a)
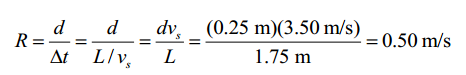
b)

9) Em uma corrida de 1 km, o corredor 1 da raia 1 (com o tempo de 2 min 27,95 s) parece ser mais
rápido que o corredor 2 da raia 2 (2 min 28,15 s). Entretanto, o comprimento L2 da raia 2 pode ser
ligeiramente maior que o comprimento L1 da raia 1. Qual é o maior valor da diferença L2 − L1 para o qual a conclusão de que o corredor 1 é mais rápido é verdadeira?


10) Para estabelecer um recorde de velocidade em uma distância d (em linha reta), um carro deve
percorrer a distância, primeiro em um sentido (em um tempo t1) e depois no sentido oposto (em um tempo t2). (a) Para eliminar o efeito do vento e obter a velocidade vc que o carro atingiria na ausência de vento, devemos calcular a média aritmética de d/t1 e d/t2 (método 1) ou devemos dividir d pela média aritmética de t1 e t2 (método 2)? (b) Qual é a diferença percentual dos dois métodos se existe um vento constante na pista, e a razão entre a velocidade vv do vento e a velocidade vc do carro é 0,0240?
(a) Suponha que, durante o intervalo de tempo t1, o carro se mova na mesma direção que o vento.
Então a velocidade efetiva do carro é dada por Veff ,1 = Vc + Vw , e a distância percorrida
é d = Veff,1t1 = (Vc + Vw)t1. Por outro lado, para a viagem de retorno durante o intervalo de tempo t2, o carro se move na direção oposta do vento e a velocidade efetiva seria Veff,2 = Vc – Vw . A distância percorrida é d = Veff,2t2 = (Vc – Vw)t2 . As duas expressões
podem ser reescrito como
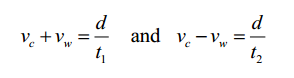
Adicionando as duas equações e dividindo por dois, obtemos
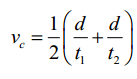
Portanto, o método 1 fornece a velocidade do carro Vc em uma situação sem vento.
(b) Se o método 2 for usado, o resultado seria
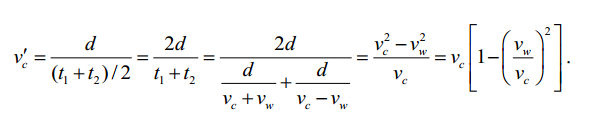
A diferença fracionária é
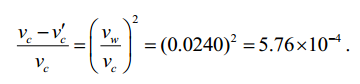
11) Você tem que dirigir em uma via expressa para se candidatar a um emprego em outra cidade, que fica a 300 km de distância. A entrevista foi marcada para as 11 h 15 min. Você planeja dirigir a 100 km/h e parte às 8 h para ter algum tempo de sobra. Você dirige à velocidade planejada durante os primeiros 100 km, mas, em seguida, um trecho em obras o obriga a reduzir a velocidade para 40 km/h por 40 km. Qual é a menor velocidade que você deve manter no resto da viagem para chegar a tempo?
Vm = 128 km/h
A entrevista é às 11:15h da manhã e ele inicia a viagem às 8 da manhã, o tempo total que ele tem para chegar é de –
ΔT = 3 horas e quinze minutos = 3,25 horas
O espaço total que ele precisa percorrer é de 300 Km.
O tempo que ele gasta nos 100 primeiros quilometros –
V = ΔS/Δt
100 = 100/Δt1
Δt1 = 1 hora
O tempo gasto nos 40 km seguintes-
Vm = ΔS/Δt
40 = 40/Δt2
Δt2 = 1 hora
O espaço que ele já percorreu em duas horas –
ΔS = 100 + 40 = 140 km
Do tempo total ele já gastou 2 horas, sobrando –
Δt = 3,25 – 2
Δt = 1,25 horas
Do espaço que ele precisa percorrer faltam –
ΔS = 300 – 140
ΔS = 160 km
A velocidade média que ele deve manter para chegar a tempo –
Vm = 160/1,25
Vm = 128 km/h
12) Onda de choque no trânsito. Quando o trânsito é intenso, uma redução brusca de velocidade
pode se propagar como um pulso, denominado onda de choque, ao longo da fila de carros. A onda de
choque pode ter o sentido do movimento dos carros, o sentido oposto, ou permanecer estacionária. A Fig. 2-25 mostra uma fila de carros regularmente espaçados que estão se movendo a uma velocidade v = 25,0 m/s em direção a uma fila de carros mais lentos, uniformemente espaçados, que estão se movendo a uma velocidade vl = 5,00 m/s. Suponha que cada carro mais rápido acrescenta um comprimento L = 12,0 m (comprimento do carro mais a distância mínima de segurança) à fila de carros mais lentos ao se juntar à fila, e que reduz bruscamente a velocidade no último momento. (a) Para que distância d entre os carros mais rápidos a onda de choque permanece estacionária? Se a distância é duas vezes maior que esse valor, quais são (b) a velocidade e (c) o sentido (o sentido do movimento dos carros ou o sentido contrário) da onda de choque?

a) Deixe os carros velozes e lentos serem separados por uma distância d em t = 0. Se durante o
intervalo de tempo t = L / Vs = (12,0 m) /(5,0 m / s) = 2,40 s em que o carro lento se moveu
uma distância de L = 12.0 m, o carro veloz move uma distância de vt = d + L para unir a linha
de carros lentos, então a onda de choque permaneceria estacionária. A condição implica
separação de
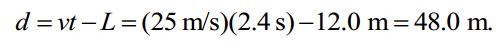
b) Deixe a separação inicial em t = 0 ser d = 96,0 m. Mais tarde, o lento e os carros velozes viajaram X = Vst e o carro rápido se une à linha movendo uma distância d + x. A partir de

nós temos

que por sua vez dá t = (24,0 m) / (5,00 m / s) 4,80 s. Desde a parte de trás do carro lento pacote deslocou uma distância de Δx = x – L = 24,0 m – 12,0 m a jusante, a velocidade da parte traseira da mochila lenta, ou equivalentemente, a velocidade da onda de choque, é
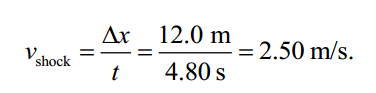
c) Como x > L, a direção da onda de choque é a jusante.
13) Você dirige do Rio a São Paulo metade do tempo a 55 km/h e a outra metade a 90 km/h. Na volta,
você viaja metade da distância a 55 km/h e a outra metade a 90 km/h. Qual é a velocidade escalar média (a) na viagem do Rio a São Paulo, (b) na viagem de São Paulo ao Rio, e (c) na viagem inteira? (d) Qual é a velocidade média na viagem inteira? (e) Plote o gráfico de x em função de t para o item (a), supondo que o movimento ocorre no sentido positivo de x. Mostre de que forma a velocidade média pode ser determinada a partir do gráfico.
Quando percorre a distância metade do tempo em cada velocidade, o tempo gasto em cada velocidade é o mesmo, logo a velocidade média será a média das velocidades.
No segundo caso, a distância percorrida em cada trecho será a mesma, logo:
Na viagem inteira, resolvemos igual a letra b, pois as distancias sao as mesmas.
No último caso, ele não pede pela velocidade escalar, mas pela velocidade média. Como ele retorna ao ponto de origem, o deslocamento é nulo, logo a velocidade média também o será.
14) A posição de um elétron que se move ao longo do eixo x é dada por x = 16te^{−t} m, em que t está em segundos. A que distância da origem está o elétron quando para momentaneamente?
Usando a propriedade geral

nós escrevemos
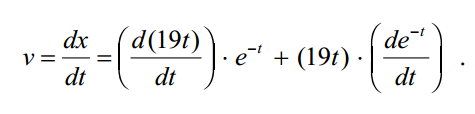
Se uma preocupação se desenvolve sobre a aparência de um argumento do exponencial (–t) aparentemente tendo unidades, então um fator explícito de 1/T where T = 1 segundo pode ser inserido e realizado através do cálculo (o que não altera a nossa resposta). O resultado dessa diferenciação é
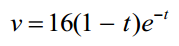
com t e v em unidades do SI (se m / s, respectivamente). Nós vemos que essa função é zero
quando t = 1 s. Agora que sabemos quando ele pára, descobrimos onde ele passa
conectando nosso resultado t = 1 na função dada x = 16te^{-t} com x em metros. Assim sendo, encontramos x = 5,9 m.
15) (a) Se a posição de uma partícula é dada por x = 4 −12t + 3t 2 (em que t está em segundos e x em metros), qual é a velocidade da partícula em t = 1 s? (b) O movimento nesse instante é no sentido positivo ou negativo de x? (c) Qual é a velocidade escalar da partícula nesse instante? (d) A velocidade escalar está aumentando ou diminuindo nesse instante? (Tente responder às duas próximas perguntas sem fazer outros cálculos.) (e) Existe algum instante no qual a velocidade se anula? Caso a resposta seja afirmativa, para que valor de t isso acontece? (f) Existe algum instante após t = 3 s no qual a partícula está se movendo no sentido negativo de x? Caso a resposta seja afirmativa, para que valor de t isso acontece?
a) A velocidade da partícula é
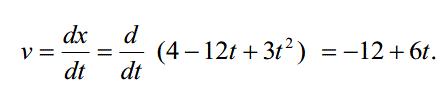
Assim, em t = 1 s, a velocidade é v = (–12 + (6) (1)) = –6 m / s.
b) Como v <0, ele está se movendo na direção –x em t = 1 s.
c) Em t = 1 s, a velocidade é | v | = 6 m / s.
d) Para 0 <t <2 s, | v | diminui até desaparecer. Para 2 <t <3 s, | v | aumenta de
zero para o valor que tinha na parte (c). Então, | v | é maior que esse valor para t> 3 s.
e) Sim, desde que v suavemente mude de valores negativos (considere o resultado t = 1) para
positivo (note que como t → + ∞, temos v → + ∞). Pode-se verificar que v = 0 quando
t = 2 s.
f) Não. De fato, de v = –12 + 6t, sabemos que v> 0 para t> 2 s.
16) A função posição x(t) de uma partícula que está se movendo ao longo do eixo x é x = 4,0 − 6,0t
2, com x em metros e t em segundos. (a) Em que instante e (b) em que posição a partícula para
(momentaneamente)? Em que (c) instante negativo e (d) instante positivo a partícula passa pela origem? (e) Plote o gráfico de x em função de t para o intervalo de −5 s a +5 s. (f) Para deslocar a curva para a direita no gráfico, devemos acrescentar a x(t) o termo +20t ou o termo −20t? (g) Essa modificação aumenta ou diminui o valor de x para o qual a partícula para momentaneamente?
Primeiro vamos derivar uma vez para achar a velocidade e depois outra vez para achar a aceleração:
Agora podemos resolver as questões:
Letra “a”: Se a partícula está parada, logo a velocidade e a aceração estão em zero.
Letra “b” : para a particular parar o seu instante tem que ser zero, logo
Letra “c” e “d”: x (t) = 0, isolamos o t para achar o resultado:
letra “e” =
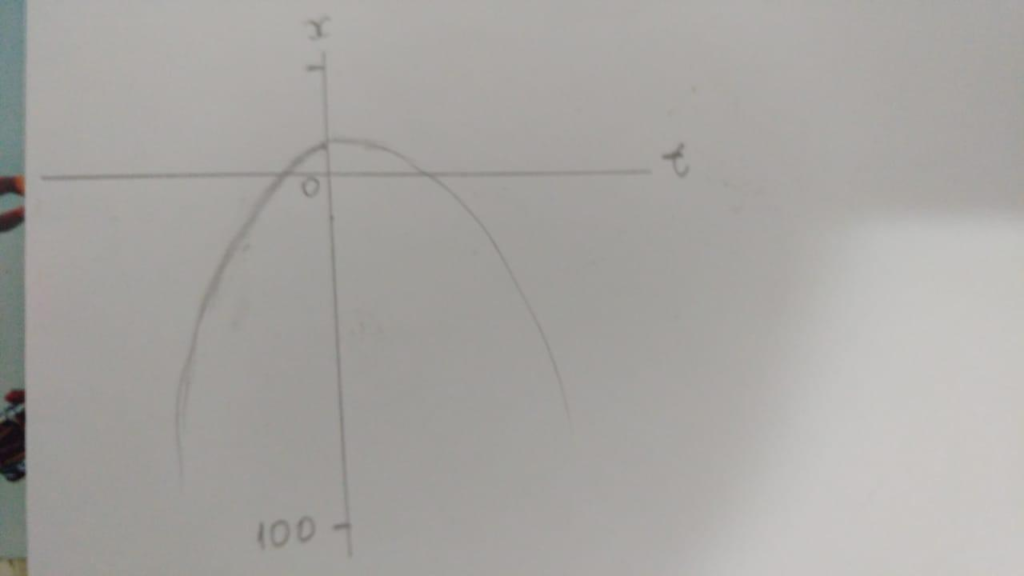
Letra “f” = para chegar no gráfico devemos colocar 20t ao x (t) da expressão.
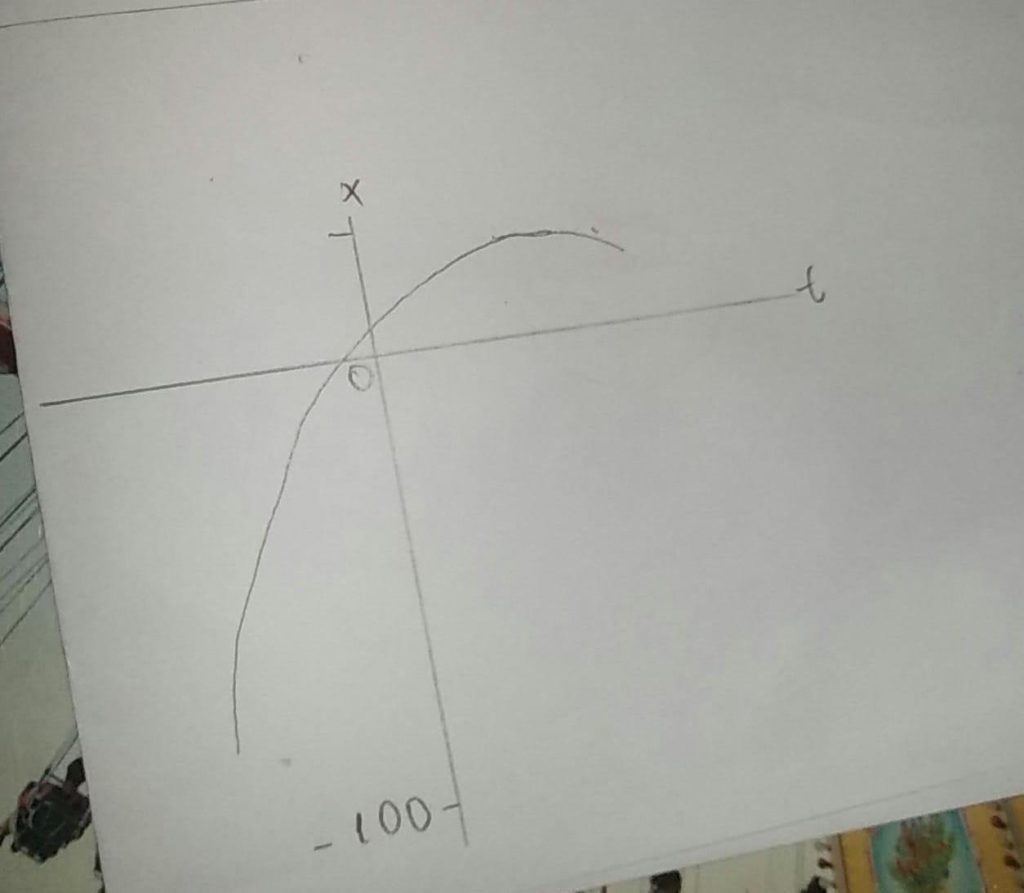
Letra “g” = Olhar onde as inclinações dos gráficos se tornam zero, é onde consta a mudança, faz com que o ponto v = 0 corresponda a um valor maior de x (o topo da segunda curva mostrado na letra “e” é maior do que o primeiro.
17) A posição de uma partícula que se move ao longo do eixo x é dada por x=9,75 + 1,50t 3, em que x está em centímetros e t em segundos. Calcule (a) a velocidade média durante o intervalo de tempo de t=2,00 s a t=3,00 s; (b) a velocidade instantânea em t=2,00 s; (c) a velocidade instantânea em t=3,00 s; (d) a velocidade instantânea em t=2,50 s; (e) a velocidade instantânea quando a partícula está na metade da distância entre as posições em t = 2,00 s e t=3,00 s. (f) Plote o gráfico de x em função de t e indique suas respostas graficamente.
A posição de uma partícula que se move ao longo do eixo x é dada em centímetros por x=9,75 + 1,50t^3, onde t está em segundos.
Calcule:
USANDO A fórmula TRADICIONAL
X= 9,75 + 1,50t³
X = Posição
a) a velocidade média entre o intervalo de tempo t = 2,00 s a t = 3,00 s
1º) ACHAR (t = 2 s) substituir (DADOS) cm
x = 9,75 + 1,50(2)³
x = 9,75 + 1,50(8)
x = 9,75 + 12
x = 21,75 cm
2º) ACHAR ( t = 3s) ( substitui) DADOS (cm)
x = 9,75 + 1,50t³
x = 9,75 + 1,50(3)³
x = 9,75 + 1,50(27)
x = 9,75 + 40,50
x = 50,25 cm
USANDO A FÓRMULA
Δxf = 50,25 ( final)
Δxi = 21,75 (inicial)
Tf = tempo final = 3s
Ti = tempo inicial = 2s
Δxf – Δxi
Vm = ————– ( substituir)
Tf – ti
50,25 – 21,75
Vm = ———————
3s – 2s
28,50 cm
Vm = —————-
1s
Vm = 28,50cm/s
b) a velocidade instantânea em t = 2,00 s.
TEMOS que devivar a EQUAÇÃO
x = 9,75 + 1,50t³
d(x)
—– = 0(9,75) + 3(1,50)t²
d(t)
d(x)
——- = 0 + 4,5t²
d(t)
d(x)
—– = 4,50t² ( sendo ( t = 2s) substituir
d(t)
d(x)
—— = 4,50(2)²
d(t)
d(x)
—— = 4,50(4)
d(t)
d(x)
—— = 18 cm/s
d(t)
18) A posição de uma partícula que se move ao longo do eixo x é dada por x = 12t^2−2t^3, em que x está em metros e t em segundos. Determine (a) a posição, (b) a velocidade e (c) a aceleração da partícula em t = 3,0 s. (d) Qual é a coordenada positiva máxima alcançada pela partícula e (e) em que instante de tempo é alcançada? (f) Qual é a velocidade positiva máxima alcançada pela partícula e (g) em que instante de tempo é alcançada? (h) Qual é a aceleração da partícula no instante em que a partícula não está se movendo (além do instante t = 0)? (i) Determine a velocidade média da partícula entre t=0 e t=3,0 s.
x = 12t² – 2t³ -> t = 3 segundos
x = 12×(3)² – 2×(3)³
x = 12×9 – 2×27
x = 108 – 54
x = 54 metros.
S = So + V×t (onde S é a posição, So o ponto inicial = 0, V é velocidade, e t é tempo)
54 = 0 + V×3
54 = 3V
3V = 54
V = 54 ÷ 3
V = 18 m/s.
V = Vo + a×t (onde V é velocidade, Vo velocidade inicial, a aceleração, e t tempo)
18 = 0 + a×3
18 = 3a
3a = 18
a = 18 ÷ 3
a = 6 m/s²
Posição = 54 metros
Velocidade = 18 m/s
Aceleração = 6 m/s²
19) Em um determinado instante, uma partícula tinha uma velocidade de 18 m/s no sentido positivo de x; 2,4 s depois, a velocidade era 30 m/s no sentido oposto. Qual foi a aceleração média da partícula durante este intervalo de 2,4 s?
Velocidade Inicial: 18 m/s²
Velocidade final: -30 m/s²
Tempo: 2,4s
Usando a função horária da velocidade Vf = Vi + a.t temos a seguinte equação:
-30 = 18 + 2,4.a
-30 – 18 = 2,4a
-48 = 2,4a
-48/2,4 = a
-20 m/s² = a
20) (a) Se a posição de uma partícula é dada por x = 20t–5t³, em que x está em metros e t em segundos, em que instante(s) a velocidade da partícula é zero? (b) Em que instante(s) a aceleração a é zero? (c) Para que intervalo de tempo (positivo ou negativo) a aceleração a é negativa? (d) Para que intervalo de tempo (positivo ou negativo) a aceleração a é positiva? (e) Desenhe os gráficos de x(t), v(t), e a(t).
a) em que instante(s) a velocidade da partícula é zero?
Para este ítem, primeiro você tem que calcular a velocidade. A velocidade é a derivada da posição, ou seja, V= dx/dt= 20-15t².
Quando ela será igual a 0?
Só substituir v por 0 na equação. V=20-15t²m/s. 0 = 20-15t². Resolvendo isso, t= +ou- 1,15s
Portanto a velocidade será 0 quando t= +ou- 1,15s.
b) em que instante(s) a aceleração da partícula é zero?
Calcular a aceleração que é a derivada da velocidade. Já calculamos a velocidade que deu 20-15t².
agora, a = dv/dt a= -30t.m/s²
Para saber quando será basta colocar zero no lugar de a na equação, 0= -30t, que nós dá t=0, ou seja, a aceleração será 0 quando t=0.
c) para que intervalo de tempo (positivo ou negativo) a aceleração é positiva?
Do resultado -30t fica fácil notar que a aceleração será positiva sempre que t for negativo. Por exemplo, se t fosse -1, substituiríamos e teríamos -30.-1= 30.
d) para que intervalo de tempo (positivo ou negativo)a aceleração é negativa?
Mesma linha de pensamento do ítem c, será negativa quando t for positivo. Se t for 1, ficará -30.1= -30
e)
21) De t = 0 a t = 5,00 min, um homem fica em pé sem se mover; de t = 5,00 min a t = 10,0 min, caminha em linha reta com uma velocidade de 2,2 m/s. Qual é (a) a velocidade média v_{méd} e (b) qual a aceleração média a_{méd} do homem no intervalo de tempo de 2,00 min a 8,00 min? (c) Qual é v_{méd} e (d) qual é a_{méd} no intervalo de tempo de 3,00 min a 9,00 min? (e) Plote x em função de t e v em função de t, e indique como as respostas de (a) a (d) podem ser obtidas a partir dos gráficos.

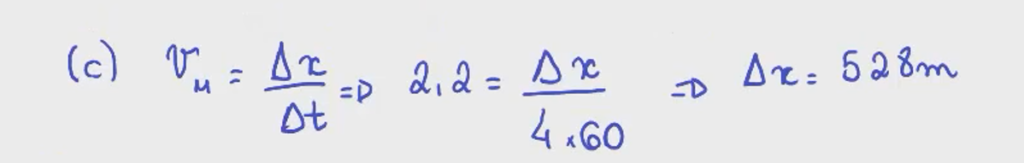

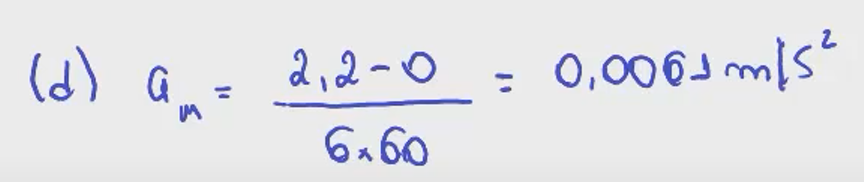
e)
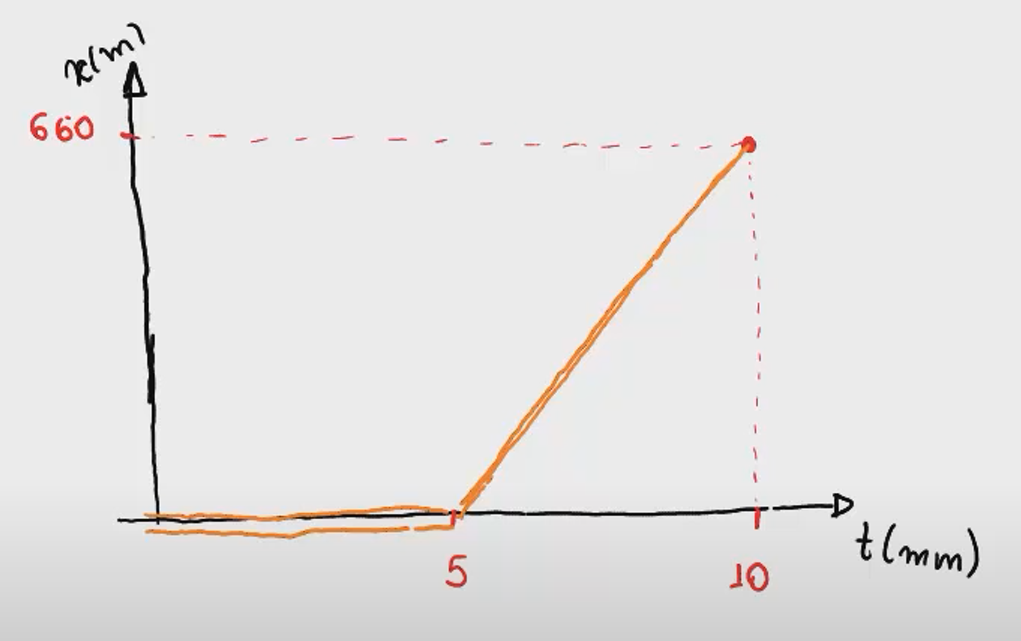
22) A posição de uma partícula que se desloca ao longo do eixo x varia com o tempo de acordo com a
equação x = ct² − bt³, em que x está em metros e t em segundos. Quais são as unidades (a) da constante c e (b) da constante b? Suponha que os valores numéricos de c e b são 3,0 e 2,0, respectivamente. (c) Em que instante a partícula passa pelo maior valor positivo de x? De t = 0,0 s a t = 4,0 s, (d) qual é a distância percorrida pela partícula e (e) qual é o deslocamento? Determine a velocidade da partícula nos instantes (f) t = 1,0 s, (g) t = 2,0 s, (h) t = 3,0 s, e (i) t = 4,0 s. Determine a aceleração da partícula nos instantes (j) t = 1,0 s, (k) t = 2,0 s, (l) t = 3,0 s e (m) t = 4,0 s.
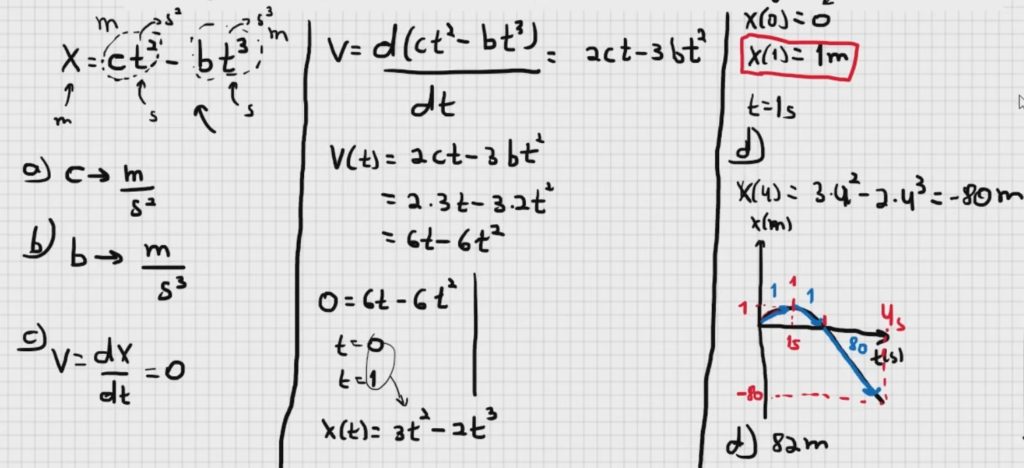

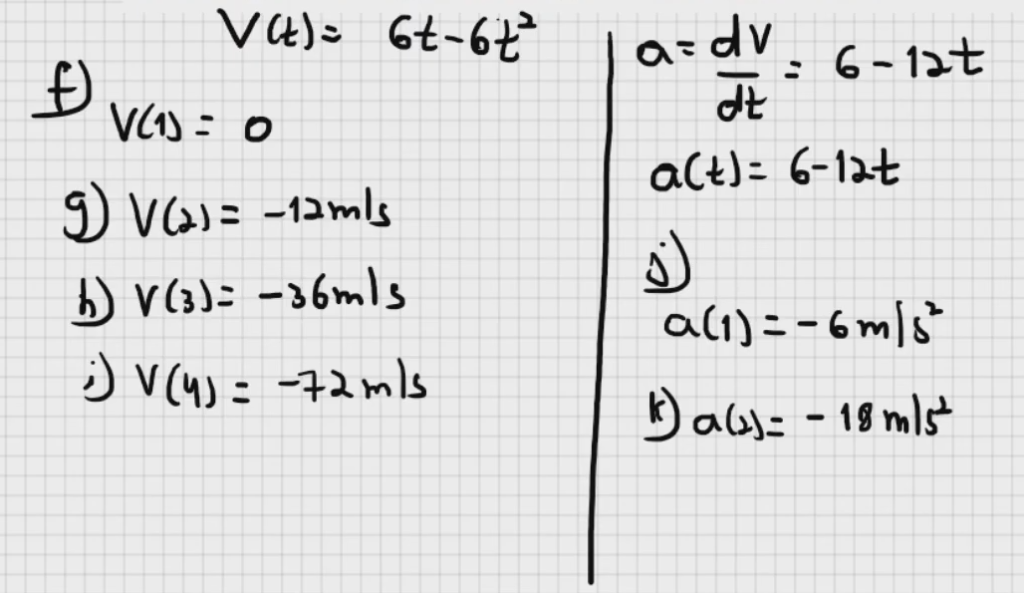
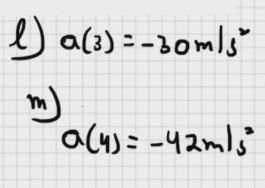
Fonte: https://www.youtube.com/watch?v=VXvFMeY-aX0
23) Um elétron com velocidade inicial v0 = 1,50 × 10 5 m/s penetra em uma região de comprimento L = 1,00 cm, em que é eletricamente acelerado (Fig. 2-26), e sai da região com v = 5,70 × 10 6 m/s. Qual é a aceleração do elétron, supondo que seja constante?

24) Cogumelos lançadores. Alguns cogumelos lançam esporos usando um mecanismo de catapulta.
Quando o vapor d’água do ar se condensa em um esporo preso a um cogumelo, uma gota se forma de um lado do esporo e uma película de água se forma do outro lado. O peso da gota faz o esporo se encurvar, mas, quando a película atinge a gota, a gota d’água se espalha bruscamente pelo filme, e o esporo volta tão depressa à posição original que é lançado no ar. Tipicamente, o esporo atinge uma velocidade de 1,6 m/s em um lançamento de 5,0 μm; em seguida, a velocidade é reduzida a zero em um percurso de 1,00 mm pelo atrito com o ar. Usando esses dados e supondo que as acelerações são constantes, determine a aceleração em unidades de g (a) durante o lançamento; (b) durante a redução de velocidade.
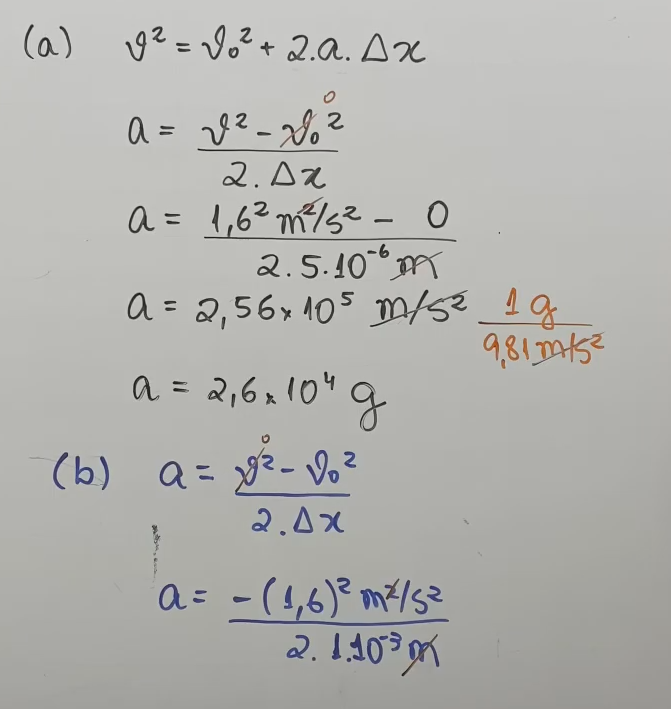
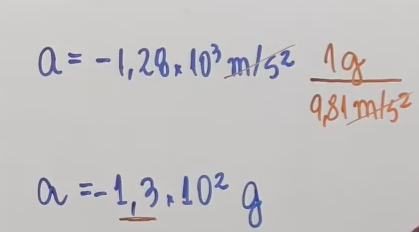
25) Um veículo elétrico parte do repouso e acelera em linha reta a uma taxa de 2,0 m/s 2 até atingir a velocidade de 20 m/s. Em seguida, o veículo desacelera a uma taxa constante de 1,0 m/s 2 até parar. (a) Quanto tempo transcorre entre a partida e a parada? (b) Qual é a distância percorrida pelo veículo desde a partida até a parada?
(a)
Em um movimento uniformemente variado, a velocidade varia uniformemente conforme o tempo passa sob a ação de uma aceleração constante.
A função horária da posição de um corpo desenvolvendo movimento retilíneo uniformemente variado segue a seguinte expressão genérica –
S = So + Vot + 1/2at²
A função horária da velocidade de um corpo desenvolvendo movimento retilíneo uniformemente variado segue a seguinte expressão genérica –
V = Vo + at
No caso em questão, temos um trecho do movimento que é acelerado e outro trecho do movimento que é retardado.
Calculando o tempo de aceleração do veículo-
V = Vo + at
20 = 0 + 2t
t = 10 segundos
Calculando o tempo de desaceleração do veículo-
V = Vo – at
0 = 20 – 1.t
t = 20 segundos
O tempo total para o veículo parar foi de-
T = 10 + 20
T = 30 segundos
Transcorrem 30 segundos entre a partida e a parada
(b)
Distância percorrida no trecho acelerado
S = So + Vot + 1/2at²
S = 0 + 0 + 1. t²
S = 10²
S = 100 metros
Distância percorrida no trecho retardado –
S = 0 + 20t – 1t²/2
S = 20. 20 – 20²/2
S = 400 – 200
S = 200 metros
Distância total percorrida até a parada-
S (total) = 100 + 200
S (total) = 300 metros
A distância percorrida pelo veículo desde a partida até a parada é de 300 metros.
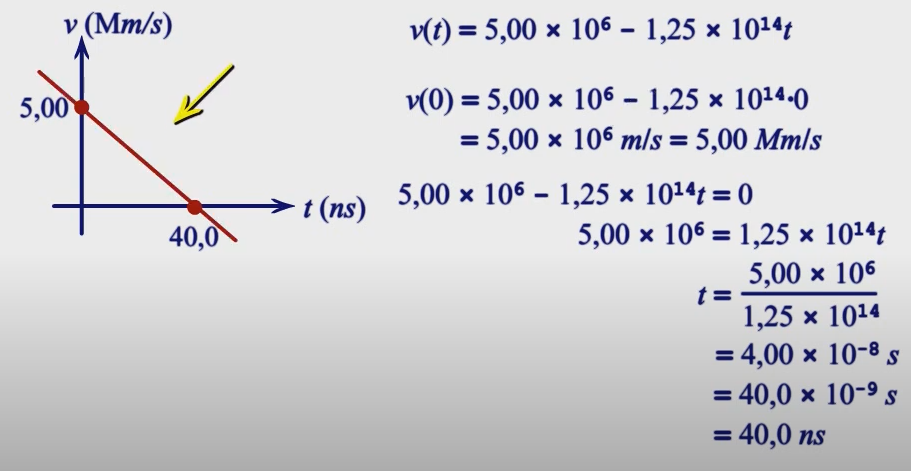
26) Um múon (uma partícula elementar) penetra em uma região com uma velocidade de 5,00 × 10
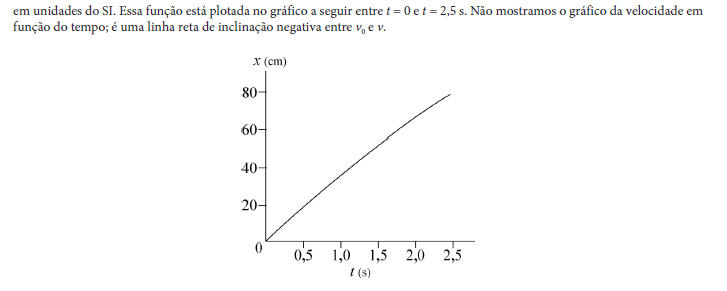
6 m/s e passa a ser desacelerado a uma taxa de 1,25 × 10_{14} m/s². (a) Qual é a distância percorrida pelo múon até parar? (b) Desenhe os gráficos de x em função de t, e de v em função de t para o múon.
a) v² = v₀² + 2a∆S
Se ele para, v = 0. v₀ = 5,00 × 10e6 m/s. a = -1,25 × 10e14 m/s².
0² = (5,00 × 10e6 m/s)² + 2(-1,25 × 10e14 m/s²)∆S
0 = (2,50 × 10e13 m²/s²) – (2,50 × 10e14 m/s²)∆S
∆S = (-2,50 × 10e13 m²/s²)/(-2,50 × 10e14 m/s²)
∆S = 0,1 m
b)
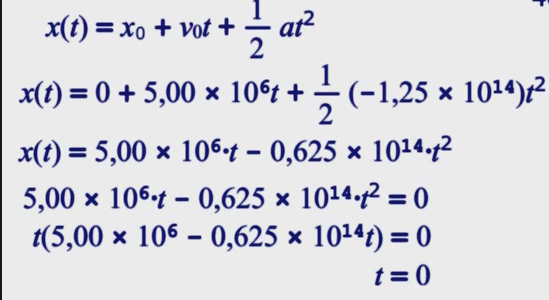
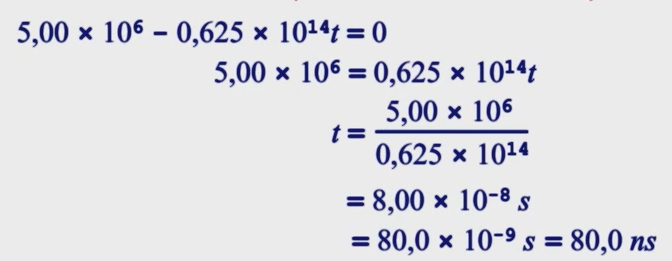

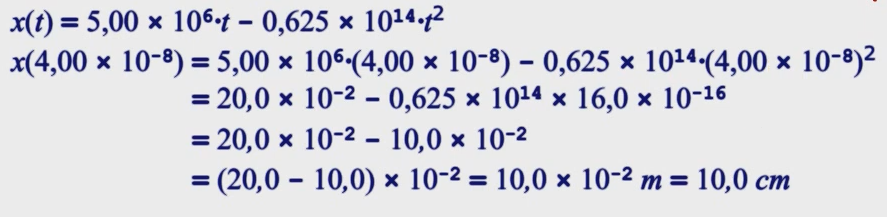

27) Um elétron possui uma aceleração constante de +3,2 m/s². Em determinado instante, a velocidade do elétron é +9,6 m/s. Qual é a velocidade (a) 2,5 s antes e (b) 2,5 s depois do instante considerado?
A velocidade de 2,5 antes é de : 3,2.0,5 = 1,6 m/s
A velocidade de 2,5 segundos depois é de: 3.2.5,5 = 1,6 m/s >>> 17,6 m/s.
Vamos aos dados/resoluções:
Sabemos que a aceleração é uma grandeza física vetorial e a mede a mudança da velocidade em relação ao tempo, logo, podemos afirmar que aceleração é a taxa de variação temporal da velocidade de um móvel. Com isso em mente;
V(t) = ∫ a.d.t
v = ∫3,2dt
v = 3,2t
é o mesmo que lembrar que v = at
9,6 = 3,2t
t = 3s
finalizando então;
A velocidade de 2,5 antes é de : 3,2.0,5 = 1,6 m/s
A velocidade de 2,5 segundos depois é de: 3.2.5,5 = 1,6 m/s >>> 17,6 m/s.
28) Em uma estrada seca, um carro com pneus novos é capaz de frear com uma desaceleração constante de 4,92 m/s². (a) Quanto tempo esse carro, inicialmente se movendo a 24,6 m/s, leva para parar? (b) Que distância o carro percorre nesse tempo? (c) Desenhe os gráficos de x em função de t, e de v em função de t durante a desaceleração.
B) Para a B, dá para usar a fórmula de Torriceli,
O V, é a velocidade final, no caso 0 pois o carro tem que parar
O Vo é a velocidade inicial, 24,6m/s no caso
O A é a aceleração, -4,92 (Negativa, pois o carro vai DESacelerar)
E temos que descobrir a distância, d
Jogando na fórmula
0² = 24,6² – 2*4,92*d
0 = 605 – 9,84d
9,84d = 605
D = 61 metros
A) Para a A, dá pra usar a fórmula V = Vo + at
V = 0
Vo = 24,6
a = – 4,92
0 = 24,6 – 4,92t
T = 5 segundos
C) Para o C, você pode usar a fórmula V =Vo + at
0 = V – 4,92a
29) Um elevador percorre uma distância de 190 m e atinge uma velocidade máxima de 305 m/min. O
elevador acelera a partir do repouso e desacelera de volta ao repouso a uma taxa de 1,22 m/s². (a) Qual é a distância percorrida pelo elevador enquanto acelera a partir do repouso até a velocidade máxima? (b) Quanto tempo o elevador leva para percorrer a distância de 190 m, sem paradas, partindo do repouso e chegando com velocidade zero?
Podemos afirmar que a cabina leva 41.6 segundos para percorrer a distância de 190 m, sem paradas, partindo do repouso e chegando com velocidade zero.
Para iniciar os cálculo, devemos admitir o uso da seguinte equação:
v= vo+ at
5,8= 0+1,22.t
t=5,8/1.22
t= 4,16 segundos
agora seguiremos utilizando a expressão abaixo:
V2= Vo² + 2.a.S
(5.8)2= 0+2 (1,22)S
S=25.8/2.44
S= 10.6 metros
Somando os três tempos aceleração e desaceleração com o tempo constante, assim:
t= 8.32 + 33.23
t= 41.6 segundos
30) Os freios de um carro podem produzir uma desaceleração da ordem de 5,2 m/s². (a) Se o motorista
está a 137 km/h e avista um policial rodoviário, qual é o tempo mínimo necessário para que o carro
atinja a velocidade máxima permitida de 90 km/h? (A resposta revela a inutilidade de frear para tentar
impedir que a alta velocidade seja detectada por um radar ou por uma pistola de laser.) (b) Desenhe os
gráficos de x em função de t, e de v em função de t durante a desaceleração.

31) Suponha que uma nave espacial se move com uma aceleração constante de 9,8 m/s², o que dá aos
tripulantes a ilusão de uma gravidade normal durante o voo. (a) Se a nave parte do repouso, quanto tempo leva para atingir um décimo da velocidade da luz, que é 3,0 × 10^8 m/s? (b) Que distância a nave percorre nesse tempo?

32) O recorde mundial de velocidade em terra foi estabelecido pelo coronel John P. Stapp em
março de 1954, a bordo de um trenó foguete que se deslocou sobre trilhos a 1020 km/h. Ele e o trenó
foram freados até parar em 1,4 s. (Veja a Fig. 2-7.) Qual foi a aceleração experimentada por Stapp
durante a frenagem, em unidades de g?


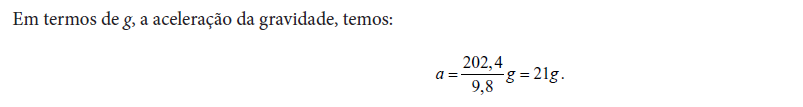
33) Um carro que se move a 56,0 km/h está a 24,0 m de distância de um muro quando o motorista aciona os freios. O carro bate no muro 2,00 s depois. (a) Qual era o módulo da aceleração constante do carro antes do choque? (b) Qual era a velocidade do carro no momento do choque?
34) Na Fig. 2-27, um carro laranja e um carro verde, iguais exceto pela cor, movem-se um em direção
ao outro em pistas vizinhas e paralelas a um eixo x. No instante t = 0, o carro laranja está em xl = 0 e o
carro verde está em xv = 220 m. Se o carro laranja tem velocidade constante de 20 km/h, os carros se
cruzam em x = 44,5 m; se tem uma velocidade constante de 40 km/h, os carros se cruzam em x = 76,6 m. (a) Qual é a velocidade inicial e (b) qual é a aceleração do carro verde?
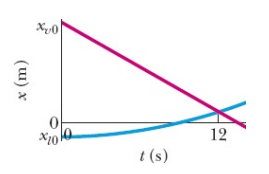
35) A Fig. 2-27 mostra um carro laranja e um carro verde que se movem um em direção ao outro. A Fig. 2-28 é um gráfico do movimento dos dois carros, mostrando suas posições xv0 = 270 m e xl0 = −35,0 m no instante t = 0. O carro verde tem velocidade constante de 20,0 m/s e o carro laranja parte do repouso. Qual é o módulo da aceleração do carro laranja?
36) Um carro se move ao longo do eixo x por uma distância de 900 m, partindo do repouso (em x = 0) e terminando em repouso (em x = 900 m). No primeiro quarto do percurso, a aceleração é +2,25 m/s². Nos outros três quartos, a aceleração passa a ser −0,750 m/s². (a) Qual é o tempo necessário para percorrer os 900 m e (b) qual é a velocidade máxima? (c) Desenhe os gráficos da posição x, da velocidade v e da aceleração a em função do tempo t.
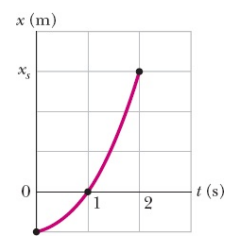
37) A Fig. 2-29 mostra o movimento de uma partícula que se move ao longo do eixo x com aceleração
constante. A escala vertical do gráfico é definida por xs = 6,0 m. Quais são (a) o módulo e (b) o sentido
da aceleração da partícula?
38) (a) Se a aceleração máxima que pode ser tolerada pelos passageiros de um metrô é 1,34 m/s² e duas estações de metrô estão separadas por uma distância de 806 m, qual é a velocidade máxima que o metrô pode alcançar entre as estações? (b) Qual é o tempo de percurso? (c) Se o metrô para durante 20 s em cada estação, qual é a máxima velocidade escalar média do metrô entre o instante em que parte de uma estação e o instante em que parte da estação seguinte? (d) Plote x, v e a em função de t para o intervalo de tempo entre o instante em que o trem parte de uma estação e o instante em que parte da estação seguinte.
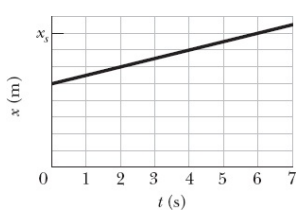
39) Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na
Fig. 2-30, do instante t = 0 ao instante t = 7,0 s. A escala vertical do gráfico é definida por x_s = 32,0 m. Em t = 0, o carro B está em x = 0, a uma velocidade de 12 m/s e com uma aceleração negativa constante a B. (a) Qual deve ser o valor de a B para que os carros estejam lado a lado (ou seja, tenham o mesmo valor de x) em t = 4,0 s? (b) Para esse valor de a B, quantas vezes os carros ficam lado a lado? (c) Plote a posição x do carro B em função do tempo t na Fig. 2-30. Quantas vezes os carros ficariam lado a lado se o módulo da aceleração a B fosse (d) maior do que o da resposta da parte (a) e (e) menor do que o da resposta da parte (a)?
40) Você está se aproximando de um sinal de trânsito a uma velocidade v0 = 55 km/h quando o
sinal fica amarelo. O módulo da maior taxa de desaceleração de que o carro é capaz é a = 5,18 m/s² e seu tempo de reação para começar a frear é T = 0,75 s. Para evitar que a frente do carro invada o cruzamento depois que o sinal mudar para vermelho, sua estratégia deve ser frear até parar ou prosseguir a 55 km/h se a distância até o cruzamento e a duração da luz amarela forem, respectivamente, (a) 40 m e 2,8 s, e (b) 32 m e 1,8 s? As respostas podem ser frear, prosseguir, tanto faz (se as duas estratégias funcionarem), ou não há jeito (se nenhuma das estratégias funcionar).
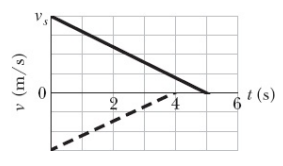
41) Os maquinistas de dois trens percebem, de repente, que estão em rota de colisão. A Fig. 2-31 mostra a velocidade v dos trens em função do tempo t enquanto estão sendo freados. A escala vertical do gráfico é definida por v_s = 40,0 m. O processo de desaceleração começa quando a distância entre os trens é 200m. Qual é a distância entre os trens quando, finalmente, conseguem parar?
42) Você está discutindo com um colega de trabalho no telefone celular enquanto, à sua frente, a 25 m
de distância, viaja um carro de polícia disfarçado; os dois veículos estão a 110 km/h. A discussão distrai
sua atenção do carro de polícia por 2,0 s (tempo suficiente para você olhar para o telefone e exclamar:
“Eu me recuso a fazer isso!”). No início desses 2,0 s, o policial freia bruscamente, com uma
desaceleração de 5,0 m/s². (a) Qual é a distância entre os dois carros quando você volta a prestar atenção no trânsito? Suponha que você leve o tempo de 0,40 s para perceber o perigo e começar a frear. (b) Se você também freia com uma desaceleração de 5,0 m/s², qual é a velocidade do seu carro quando você bate no carro de polícia?
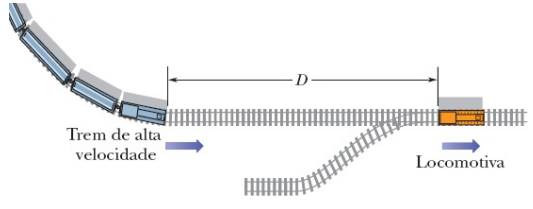
43) Quando um trem de passageiros de alta velocidade que se move a 161 km/h faz uma curva, o
maquinista leva um susto ao ver que uma locomotiva entrou indevidamente nos trilhos através de um
desvio e está a uma distância D = 676 m à frente (Fig. 2-32). A locomotiva está se movendo a 29,0 km/h. O maquinista do trem de alta velocidade imediatamente aciona os freios. (a) Qual deve ser o valor mínimo do módulo da desaceleração (suposta constante) para que a colisão não ocorra? (b) Suponha que o maquinista está em x = 0 quando, no instante t = 0, avista a locomotiva. Desenhe as curvas de x(t) da locomotiva e do trem de alta velocidade para os casos em que a colisão é evitada por pouco e em que a colisão ocorre por pouco.
44) Um tatu assustado pula verticalmente para cima, subindo 0,544 m nos primeiros 0,200 s. (a) Qual é a velocidade do animal ao deixar o solo? (b) Qual é a velocidade na altura de 0,544 m? (c) Qual é a altura adicional que o animal atinge?
45) (a) Com que velocidade deve ser lançada uma bola verticalmente a partir do solo para que atinja uma altura máxima de 50 m? (b) Por quanto tempo a bola permanece no ar? (c) Esboce os gráficos de y, v e a em função de t para a bola. Nos dois primeiros gráficos, indique o instante no qual a bola atinge a altura de 50 m.




