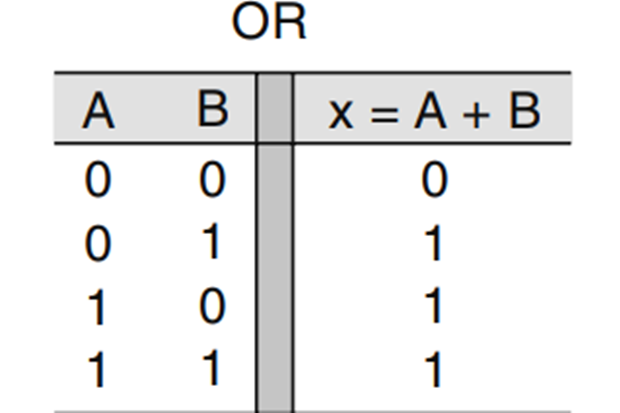
Faremos uma análise da simplificação de circuitos lógicos usando álgebra booleana. É necessário que entendamos o funcionamento das portas AND e OR, dessa forma poderemos simplificar o sitema em soma de produtos ou produto de somas, por exemplo:
Apesar de que a forma “produto de somas” utilizaremos em estruturas particulares de circuitos lógicos.
As simplificações são importantes pois agiliza e evita qualquer atraso de propagação de sinal do sistema. Conseguimos fazer a simplificação usando métodos como o distributivo, associativo, identidade e etc. Quando tentarmos simplificar, é normal que encontremos dificuldade de identificar qual teorema deve ser mais eficaz. Para que fique claro a importância da simplificação, vamos ver um exemplo onde notaremos sua importância.
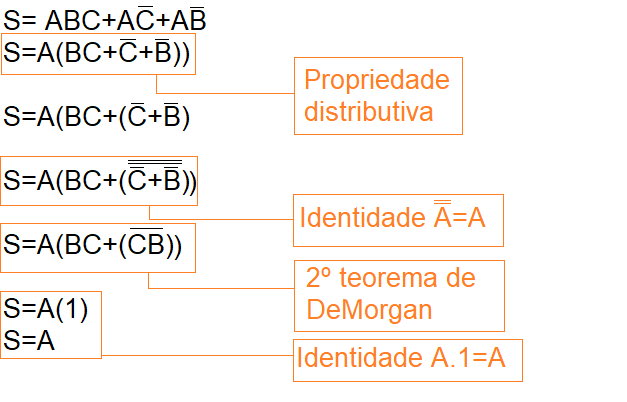
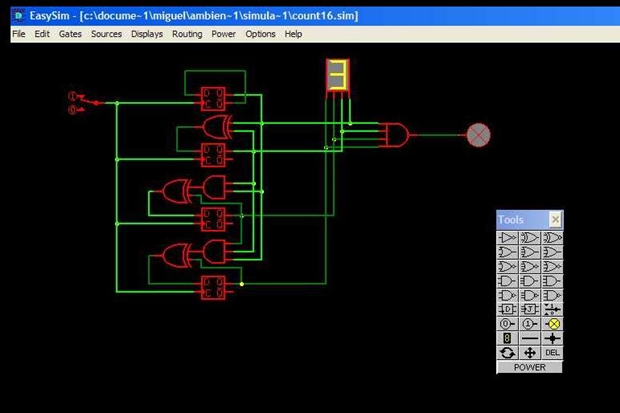
Fazendo uma simulação do sistema, teremos:
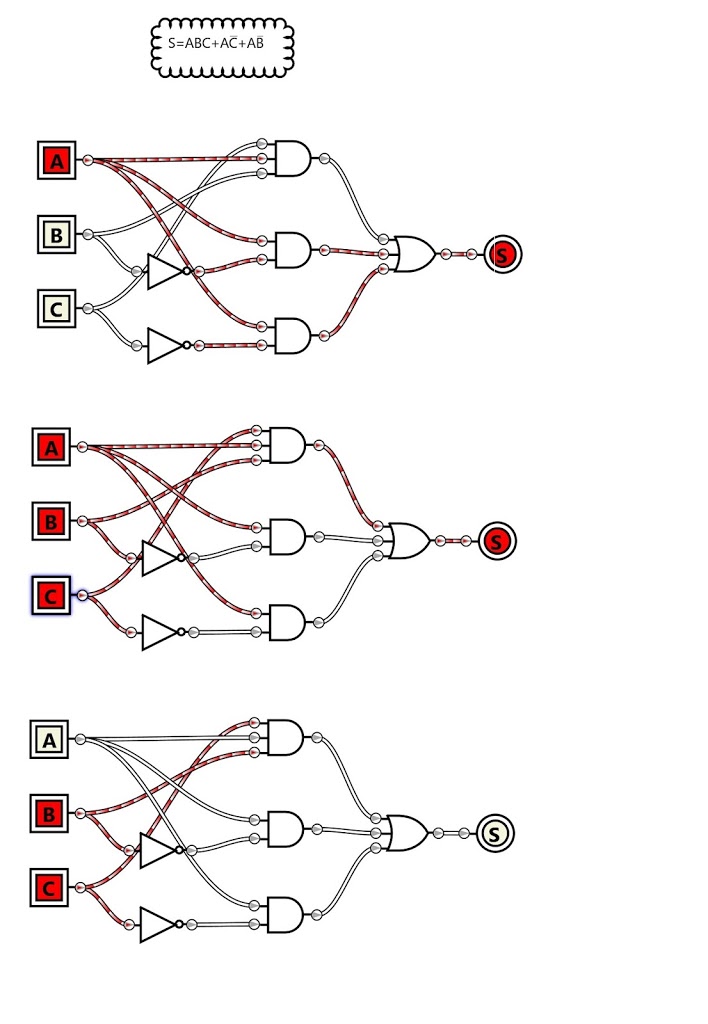
Perceba a dependência da saída alta com a entrada A.
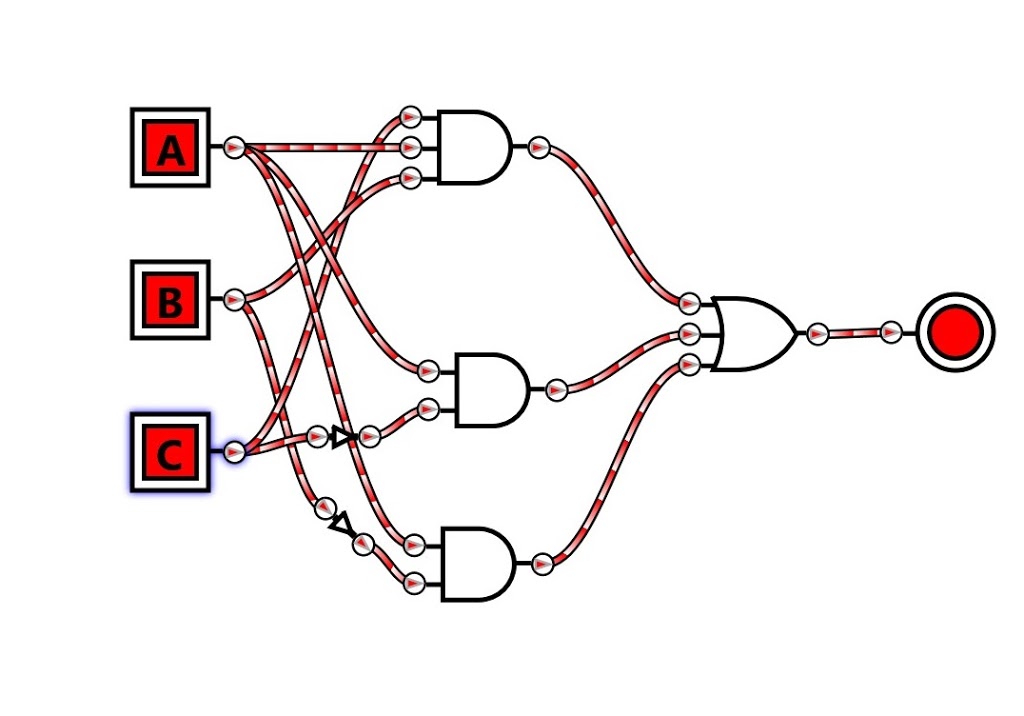
Após nossa simplificação resumimos isso em:
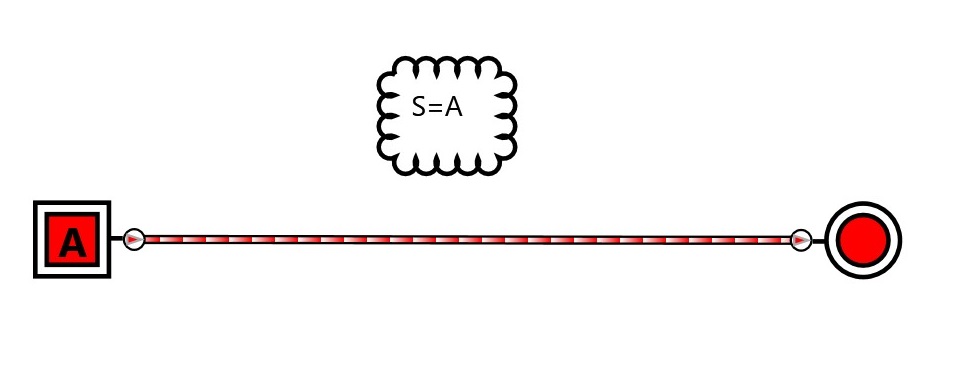
Simplificar tornará o sistema mais econômico e dará mais velocidade.
Fácil, né? Qualquer dúvida use os comentários!
Neste exemplo utilizei o programa Logic Gate Simulator 1.4. Clique aqui e faça o download.
Inscrever-se
0 Comentários
mais antigos