Água flui para baixo ao longo de um tubo inclinado de 30º em relação à horizontal conforme mostrado. A diferença de pressão p_A - p_B é causada parcialmente pela gravidade e parcialmente pelo atrito. Deduza uma expressão algébrica para a diferença de pressão. Calcule a diferença de pressão se L=1,5 m e h = 150 mm .
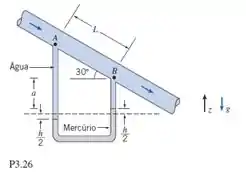
Passo 1
Para a gente organizar os pensamentos e marcar os pontinhos, vamos fazer um esqueminha!!
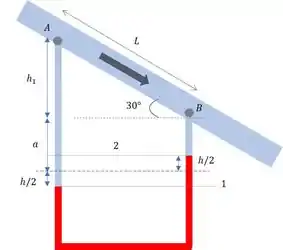
MEU DEUS, TEM ÂNGULO, O QUE EU VOU FAZER???!!
Sabendo que:
\Delta p=\rho g \Delta h
Aqui a gente tem vasos comunicantes, então sempre que eu tiver um mesmo líquido em uma mesma altura as pressões vão ser iguais!
Calculando p_1 pelo lado esquerdo:
p_1=\rho_{\text {água }} g\left(\dfrac{h}{2}+a\right)+\rho_{\text {água }} g h_1+p_a
Agora pelo lado direito:
p_1=\rho_{H g} g\left(\dfrac{h}{2}+\dfrac{h}{2}\right)+\rho_{\text {água }} g\left(a-\dfrac{h}{2}\right)+p_b
Igualando:
\rho_{\text {água }} g\left(\dfrac{h}{2}+a\right)+\rho_{\text {água }} g h_1+p_a=\rho_{H g} g\left(\dfrac{h}{2}+\dfrac{h}{2}\right)+\rho_{\text {água }} g\left(a-\dfrac{h}{2}\right)+p_b
Sabendo que:
\rho=S G \rho_w
Agora a gente vai substituir e dar uma organizadinha na nossa expressão:
\left.p_a-p_b=\rho_{\text {água }} g\left(h\left(S G_{H g}-1\right)-h_1\right)\right)
Agora sim, quem é h_1 ??!! Reparou que a gente tem um triângulo? Então a gente pode dizer que:
\sin 30^{\circ}=\dfrac{h_1}{L}
Substituindo:
p_a-p_b=\rho_{\text {água }} g\left(h\left(S G_{H g}-1\right)-\mathrm{L} \sin 30^{\circ}\right)
Awee!!!
Passo 2
Agora a gente tem que substituir!!
Sabendo que:
\rho_{\text {agua }}=1000 \mathrm{~kg} / \mathrm{m}^3
S G_{H_g}=13,55
g=9,81
\sin 30^{\circ}=0,5
L=1,5 \mathrm{~m}
h=150 \mathrm{~mm}=0,150 \mathrm{~m}
Usando a expressão que achamos:
\left.\Delta P=\rho_{a_{y u a}} g\left(h\left(S G_{H g}-1\right)-\mathrm{L} \sin 30^{\circ}\right)\right)
Substituindo e calculando:
\Delta P=1000 \times 9,81(0,150(13,55-1)-(1,5 \times 0,5)))=11110 P a
Ou:
\Delta P=11,1 k P a
Resposta
\Delta P=11,1 k P a

