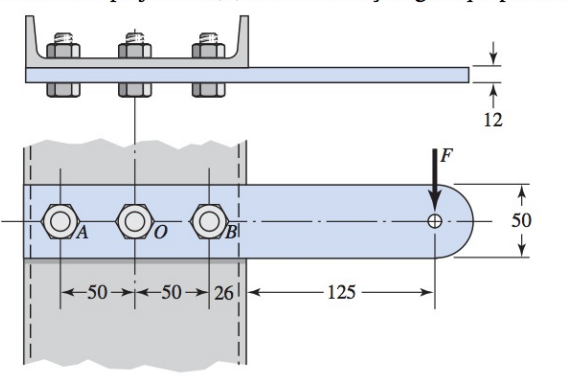
Um canal vertical 152 x 76 (ver Tabela A-7) tem uma viga em balanço parafusada a ele como mostra a figura. O canal é de aço AISI 1006 laminado a quente. A barra é de aço AISI 1015 laminado a quente. Os parafusos de ressalto são M10 x 1,5 ISO 5,8. Admita que a rosca dos parafusos não se estende para o interior da junta. Para um fator de projeto de 2,0, encontre a força segura que pode ser aplicada à viga em balanço.
Resposta
Primeiro, iremos buscar as resistências S_y dos elemenos.
Parafusos, pela tabela 8-11, S_y = 420 MPa
Canal, pela tabela A-20, S_y = 170 MPa. Pela tabela A-7, t = 6,4 mm
Viga, pela tabela A-20, S_y = 190 MPa

Pelo diagrama de corpo livre, temos que
F'_A = F'_B = F'_C = \dfrac{F}{3}
M = ( 50 + 26 + 125 ) = 201 F
F''_A = F''_C = \dfrac{201F}{2*50} = 2,01F
Força máxima,
F''_A = F'_C + F''_C = ( \dfrac{1}{3} + 2,01 )F= 2,343 F
Cisalhamento nos parafusos:
S_{sy } = 0,577*420 = 242,3 KPa
A_s = \dfrac{\pi 10^2}{4} = 78,54 mm^2
\tau_{max }= \dfrac{F_C}{A_S} = \dfrac{S_{sy }}{n}
Substituindo F_C,
F = \dfrac{S_y}{n} \left(\dfrac{A_s}{2,343}\right) = \dfrac{242,3}{2,0} \left(\dfrac{78,54}{2,343}\right) * 10^{-3} = 4,06 kN
Carga no parafuso:
A_b = td = 6,4*10 = 64 mm^2
F = \dfrac{S_y}{n} \left(\dfrac{A_b}{2,343}\right) = \dfrac{420}{2,0} \left(\dfrac{64}{2,343}\right) * 10^{-3} = 5,74 kN
Carga no canal:
A_b = 64 mm^2
F = \dfrac{S_y}{n} \left(\dfrac{A_b}{2,343}\right) = \dfrac{170}{2,0} \left(\dfrac{64}{2,343}\right) * 10^{-3} = 2,32 kN
Carga na viga:
A_b = 12*10 = 120 mm^2
F = \dfrac{S_y}{n} \left(\dfrac{A_b}{2,343}\right) = \dfrac{190}{2,0} \left(\dfrac{120}{2,343}\right) * 10^{-3} = 4,87 kN
Flexão da viga em C:
I = \dfrac{1}{12}*12*(50^3-10^3) = 1,24*10^5 mm^4
\sigma_{max} \dfrac{S_y}{n} = \dfrac{Mc}{I} = \dfrac{151Fc}{I} \implies F = \dfrac{S_y}{n} \left( \dfrac{I}{151c} \right)
F = \dfrac{190}{2,0} \left[ \dfrac{1,24*10^5}{151*25} \right]*10^{-3} = 3,12 kN
Assim, a carga que pode ser aplicada na viga é de F = 2,32 kN.

