87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético \vec {B} não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para dentro do eixo O_z . O componente z é dado por B_z (z) = \beta z , em que \beta é uma constante positiva. O componente radial B_r depende somente de r, a distância radial até o eixo O_z.
a) Use a Lei de Gauss para o magnetismo, dada pela Equação (27.8), para determinar o componente B_r em função de r. (Sugestão: experimente uma superfície gaussiana cilíndrica de raio r concêntrica com o eixo O_z, com uma extremidade em z=0 e a outra no ponto z=L).
b) Faça um desenho mostrando as linhas do campo magnético.
Passo 1
A equação 27.8 nos diz que:
\oint \vec{B} \cdot \overrightarrow{d A}=0
Então é como se tivéssemos que a somatória dos fluxos magnéticos em todas as área é igual a zero, e o corpo cilíndrico é composto por três áreas. Que são as duas áreas circulares de cima e a de baixo mas o seu corpo, porém não vamos contar o fecho circular de baixo pois a componente z do campo magnético será nulo, o que nos deixa com:
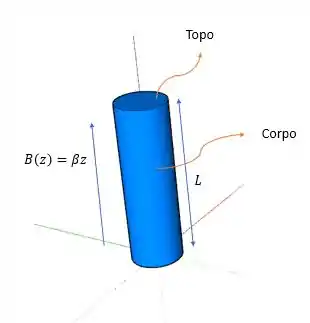
\sum \vec{B} \cdot \vec{A}=B_{\text {topo }} \cdot A_{\text {topo }}+B_{\text {corpo }} \cdot A_{\text {corpo }}
Onde B_{\text {topo }}=\beta L ; A_{\text {topo }}=\pi r^2 e B_{\text {corpo }}=\beta_r ; A_{\text {corpo }}=L \times 2 \pi r
Pois a componente radial \beta_r depende somente do raio do corpo.
Então:
\sum \vec{B} \cdot \vec{A}=\beta L \times \pi r^2+\beta_r \times L 2 \pi r=0
Então \beta , valerá
\beta_r = -\dfrac{\beta L\pi r^2}{2 \pi r L} = -\dfrac {\beta}{2}
Passo 2
Visto no plano x - y nós temos:
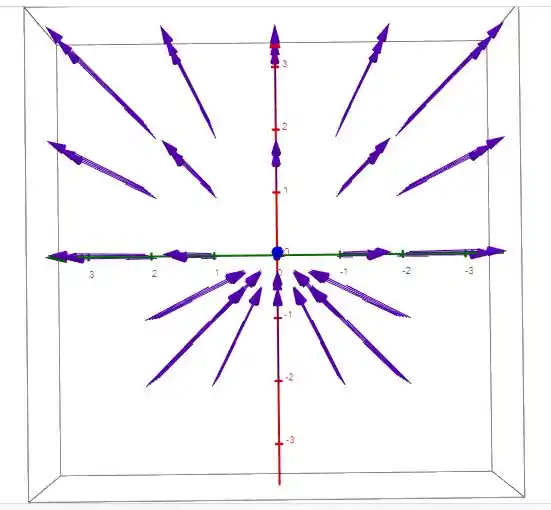
E vendo o eixo z nós temos:
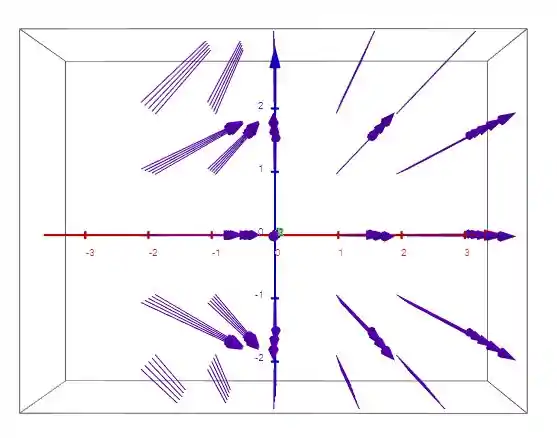
Um possível campo magnético possível é:
B=\left[\left(x^2+y^2\right)^{\frac{1}{2}} \operatorname{sen}\left(\tan ^{-1} \dfrac{y}{x}\right)\right] i+\left[\left(x^2+y^2\right)^{\frac{1}{2}} \cos \left(\tan ^{-1} \dfrac{y}{x}\right)\right] j+\beta z k
Resposta
a) \beta_r=-\dfrac{\beta r}{2}
b) Passo 2

