O óculos é uma invenção datada do século XVII, com melhorias posteriores por Benjamin Franklin, em 1785, que inventou os primeiros óculos bifocais para enxergar de longe e de perto.
Dependendo da necessidade do usuário, a lente terá um formato diferente. Podemos dividir essas lentes em convergentes e divergentes:
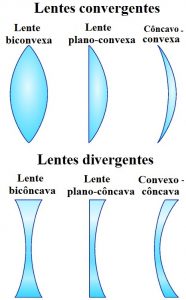
Todas as lentes que têm a parte central mais grossa que as bordas são convergentes, as que têm as bordas mais grossas que a parte central são lentes divergentes. As lentes de óculos apresentam comportamento parecido com o dos espelhos, sendo que os raios são agora refratados ao invés de refletidos.
Entendendo a refração em uma superfície esférica
A refração da luz é o fenômeno que ocorre quando a luz muda seu meio de propagação. Consideremos dois meios transparentes ![]() e
e ![]() , sendo R a fronteira entre eles. Vamos admitir O como o objeto no meio do índice de refração
, sendo R a fronteira entre eles. Vamos admitir O como o objeto no meio do índice de refração ![]() e I o ponto imagem.
e I o ponto imagem.
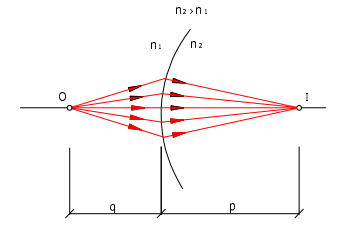
Geometricamente:
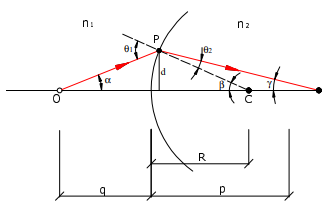
Se analisarmos a construção geométrica da Figura 3, pela lei de Snell temos:
![]() sen
sen![]() =
= ![]() sen
sen![]()
Levando em consideração que os ângulos ![]() e
e ![]() são pequenos, utilizaremos a aproximação sen
são pequenos, utilizaremos a aproximação sen![]() ~
~ ![]() e sen
e sen![]() ~
~ ![]() , assim:
, assim:
![]() θ_1 =
θ_1 = ![]() θ_2
θ_2
O ângulo externo de um triângulo qualquer é igual a soma dos ângulos internos não adjacentes ao lado oposto, assim, observando o triângulo OPC, temos:
![]()
![]()
Considerando as três últimas equações, temos que:
![]()
Também considerando tgθ ~ θ, podemos descrever:
![]()
Onde d é a distância. Se utilizarmos essa igualdade na equação anterior, temos:
![]()
Equação dos fabricantes de lentes (Equação de Halley)
![]()
No PDF abaixo mostro a Construção de imagens em lentes esféricas:
lentePara entender o comportamento de cada tipo de lente no olho humano, precisamos também entender o que há no olho que necessite dessa especificidade.
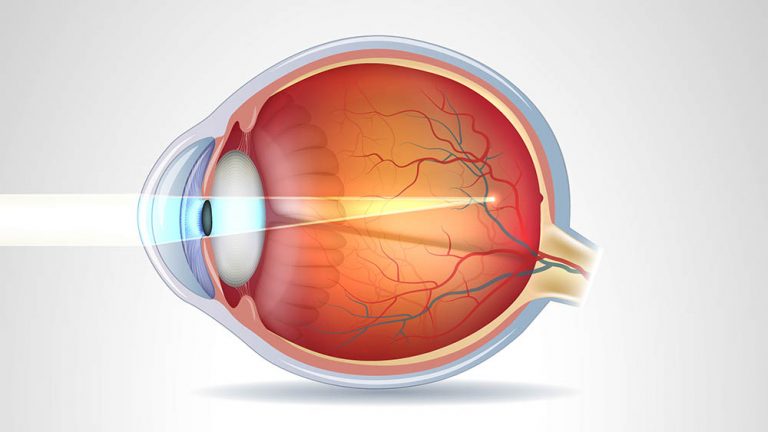
A miopia é caracterizada por um globo ocular mais “longo”, o que provoca a formação da imagem antes que a luz chegue até a retina. O problema é corrigido com lentes divergentes (côncavas). Como a luz pode incidir por dois lados, agora temos dois focos. Em uma lente bicôncava, por exemplo, o segundo raio diverge do eixo e seu prolongamento para trás intercepta o primeiro raio, formando aí uma imagem virtual do objeto.
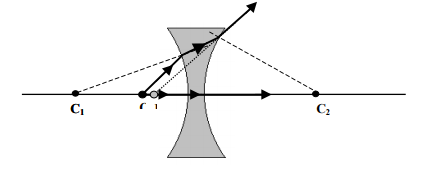
C1 e C2 são os centros de curvatura das superfícies. Observe a imagem abaixo, se você puser o objeto em outras distâncias e construir as imagens, poderá verificar que em uma lente divergente elas sempre serão virtuais, direitas e menores.
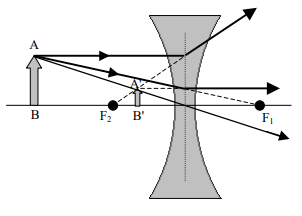
O foco (F1 e F2) da lente divergente pode ser encontrado através da equação:
![]()
Onde,
f – Foco da lente divergente (para lente divergente f < 0)![]() – Imagem Real
– Imagem Real![]() – Imagem Virtual
– Imagem Virtual
Reforçando:
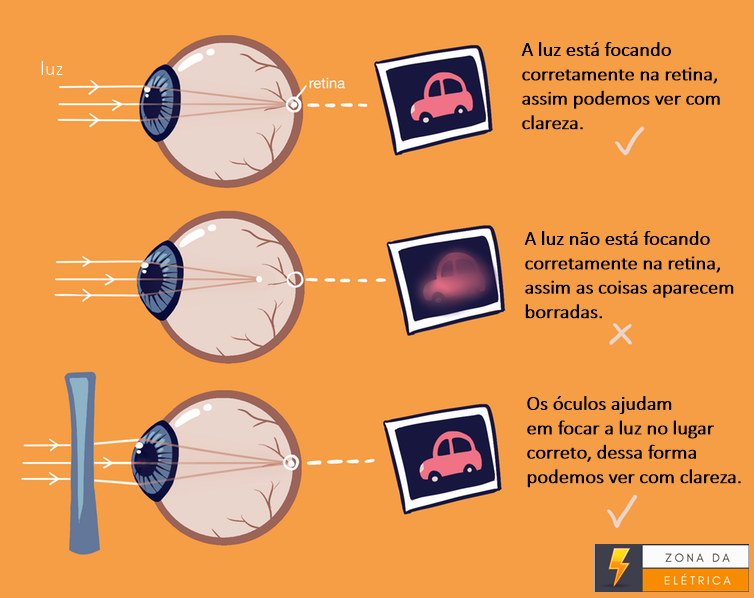
A hipermetropia é o oposto da miopia, ou seja, o olho é mais “curto”, o que faz com que a imagem se forme depois da retina.
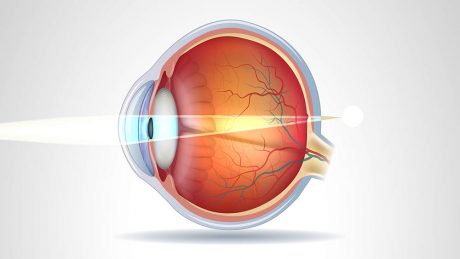
Para esse tipo de olho a lente de óculos utilizada é a convergente (convexa). A formação da imagem em uma lente convergente é real e invertida. A medida que afastamos o objeto do F sua imagem irá aumentar ou diminuir. Esse mesmo tipo de lente é utilizada em projetores de cinema, projetores de transparência e etc.
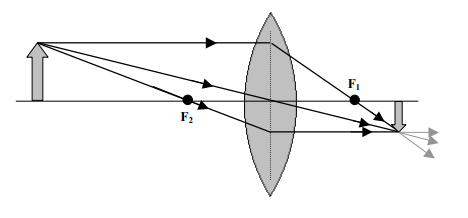
Levando em consideração que sempre estaremos trabalhando com lentes delgadas (lente onde pelo menos um lado tem uma curvatura), podemos associar os eixos principais das lentes onde elas se coincidem. Podemos associar lentes esféricas de duas maneiras:
Justaposição: associação de lentes. Dessa maneira, precisamos de uma lente equivalente às lentes associadas. Para isto o Teorema das Vergências diz que “A vergência das lentes justapostas é igual a soma algébrica das vergências das lentes individuais”. Matematicamente:
![]()
onde,
![]() é a vergência da lente equivalente;
é a vergência da lente equivalente;
![]() é a vergência da lente 1;
é a vergência da lente 1;
![]() é a vergência da lente 2.
é a vergência da lente 2.
A outra maneira seria ignorar uma lente e usar apenas uma, tratando a imagem formada como objeto. Dessa forma utilizaríamos a equação:
![]()
já citada anteriormente.
REFERÊNCIAS
[1] Introdução às ciências físicas 1 / Maria Antonieta T. de Almeida. – 3ª ed. – Rio de Janeiro: Fundação CECIERJ, 2009
[2] https://drauziovarella.uol.com.br/doencas-e-sintomas/miopia-hipermetropia-e-astigmatismo/
[3] https://brasilescola.uol.com.br/fisica/lentes-1.htm