Elementos de máquinas – Shigley 10° Ed – Capítulo 10 – Ex.20

Considere a mola de aço especial na ilustração.
(a) Encontre o passo, a altura sólida e o número de voltas ativas.
(b) Encontre a razão de mola. Suponha que o material seja aço A227 HD (estirado a frio).
(c) Encontre a força F_srequerida para fechar a mola a sólido.
(d) Encontre a tensão de cisalhmaneto na mola devido à força F_s.

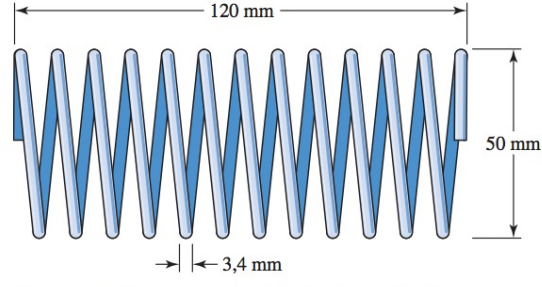
Solução

(a)

Contando as espiras, temos que N_t = 12, 5 \; espiras. Como se trata de uma mola com as extremidades esquadradas, temos 0,25 \; espiras \; em cada ponta.

Assim,

N_a = 12,5 - 0,5 = 12\;espiras

p = \dfrac{120}{12} = 10 mm

L_s = d(N_a +1) = 3,4*(12+1) \implies L_s = 44,2 mm

(b)

Da tabela 10-5:

d = \dfrac{3,4}{25,4} = 0,1339 in \implies G = 78,6 \; GPa

k = \dfrac{d^4 G}{8D^3 N_a} = \dfrac{3,4^4 * 78,6*10^9}{8*46,6^3 *12}*10^{-3} = 1080 \; \dfrac{N}{m}

(c)

F_s = k(L_0 - L_s) = 1080*(120 - 44,2)*(10^{-3}) = 81,9 \;N

(D)

C = \dfrac{D}{d} = \dfrac{46,6}{3,4} = 13,71

K_B= \dfrac{4*13,71 + 2}{4*13,71 - 3} = 1,096

\tau_{s} = \dfrac{8K_B F_s D}{\pi d^3} = \dfrac{8*1,096*81,9*46,6}{\pi *3,4^3} = 271 \;MPa