Calcule
J=\iiint_W z^2 d x d y d z
Onde W={(x, y, z) \in \mathbb{R}^3 \mid x^2+y^2+z^2 \geq 1, x^2+y^2+(z-2)^2 \leq 4 e z \geq \sqrt{x^2+y^2}}
Passo 1
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.

Temos uma esfera de raio \rho=1 centrada na origem, em azul, e outra de raio 2 centrada em (0,0,2), em verde. Temos a folha superior de um cone (pois a raiz deve ser positiva).
Queremos a região que está fora da esfera de raio 1 (pois o enunciado pede x^2+y^2+z^2 \geq 1 ), dentro da esfera de raio 2 (pois temos \left.x^2+y^2+(z-2)^2 \leq 4\right) e, ao mesmo tempo, acima do cone \left(z \geq \sqrt{x^2+y^2}\right). Fazendo esses cortes, teremos então:
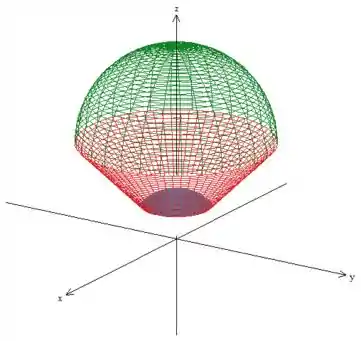
Passo 2
Como a região é limitada por duas esferas e um cone, vamos utilizar coordenadas esféricas:
x=\rho \operatorname{sen} \varphi \cos \theta
y=\rho \operatorname{sen} \varphi \operatorname{sen} \theta
z=\rho \cos \varphi
|J|=\rho^2 \operatorname{sen} \varphi
Passo 3
Precisamos agora escrever matematicamente a região de integração.
Pela própria figura, já vemos que 0 \leq \theta \leq 2 \pi (uma volta completa em torno de z ). Os valores de \rho, nós vemos que variam desde a superfície da esfera menor até a da esfera maior. A esfera menor, como está centrada na origem, pode ser escrita como \rho=1. Precisamos, então, fazer a mudança de coordenadas na equação da esfera maior:
(\rho \operatorname{sen} \varphi \cos \theta)^2+(\rho \operatorname{sen} \varphi \operatorname{sen} \theta)^2+(\rho \cos \varphi-2)^2=4
\left(\rho^2 \operatorname{sen}^2 \varphi\right) \cos ^2 \theta+\left(\rho^2 \operatorname{sen}^2 \varphi\right) \operatorname{sen}^2 \theta+\rho^2 \cos ^2 \varphi-4 \rho \cos \varphi+4=4
\rho^2 \operatorname{sen}^2 \varphi+\rho^2 \cos ^2 \varphi=4 \rho \cos \varphi
\rho=4 \cos \varphi
Temos, então 1 \leq \rho \leq 4 \cos \varphi.
Falta agora o intervalo de \varphi. Pela figura, vemos que esse ângulo varia desde o eixo z, onde temos \varphi=0 até a superfície do cone. Vamos, então, escrever a equação desse cone em coordenadas esféricas:
\rho \cos \varphi=\sqrt{(\rho \operatorname{sen} \varphi \cos \theta)^2+(\rho \operatorname{sen} \varphi \operatorname{sen} \theta)^2}
\rho \cos \varphi=\sqrt{\left(\rho^2 \operatorname{sen}^2 \varphi\right) \cos ^2 \theta+\left(\rho^2 \operatorname{sen}^2 \varphi\right) \operatorname{sen}^2 \theta}
\rho \cos \varphi=\sqrt{\rho^2 \operatorname{sen}^2 \varphi}=\rho \operatorname{sen} \varphi
\operatorname{sen} \varphi=\cos \varphi \rightarrow \operatorname{tg} \varphi=1 \rightarrow \varphi=\pi / 4
Portanto, 0 \leq \varphi \leq \pi / 4. A região será escrita como:
W={(\rho, \theta, \varphi) \mid 0 \leq \theta \leq 2 \pi ; 0 \leq \varphi \leq \pi / 4 ; 1 \leq \rho \leq 4 \cos \varphi}
Passo 4
Vamos agora substituir os intervalos que encontramos na integral iterada:
\int_0^{\pi / 4} \int_0^{2 \pi} \int_1^{4 \cos \varphi}(\rho \cos \varphi)^2 \rho^2 \operatorname{sen} \varphi d \rho d \theta d \varphi=
=\int_0^{\pi / 4} \int_0^{2 \pi} \int_1^{4 \cos \varphi} \rho^4 \cos ^2 \varphi \operatorname{sen} \varphi d \rho d \theta d \varphi=
Passo 5
Agora integraremos em relação a \rho:
=\left.\int_0^{\pi / 4} \int_0^{2 \pi} \dfrac{\rho^5}{5} \cos ^2 \varphi \operatorname{sen} \varphi\right\vert_{\rho=1}^{\rho=4\cos\varphi} d \theta d \varphi=
=\frac{1}{5} \int_0^{\pi / 4} \int_0^{2 \pi} 4^5 \cos ^7 \varphi \operatorname{sen} \varphi-\cos ^2 \varphi \operatorname{sen} \varphi d \theta d \varphi=
Passo 6
Agora vamos integrar em relação a \theta:
=\left.\dfrac{1}{5} \int_0^{\pi / 4}\left(4^5 \cos ^7 \varphi \operatorname{sen} \varphi-\cos ^2 \varphi \operatorname{sen} \varphi\right) \theta\right|_{\theta=0} ^{\theta=2 \pi} d \varphi=
=\dfrac{2 \pi}{5} \int_0^{\pi / 4} 4^5 \cos ^7 \varphi \operatorname{sen} \varphi-\cos ^2 \varphi \operatorname{sen} \varphi d \varphi=
=\dfrac{2 \pi}{5}\left[\int_0^{\pi / 4} 4^5 \cos ^7 \varphi \operatorname{sen} \varphi d \varphi-\int_0^{\pi / 4} \cos ^2 \varphi \operatorname{sen} \varphi d \varphi\right]=
Passo 7
Vamos calcular separadamente cada integral. Para a 1^{\mathrm{a}}, faremos:
\cos ^8 \varphi=u
-8 \operatorname{sen} \varphi \cos ^7 \varphi d \varphi=d u
\cos 0=1 \rightarrow u=1
\cos \pi / 4=\dfrac{\sqrt{2}}{2} \rightarrow u=1 / 16
\int_0^{\pi / 4} 4^5 \cos ^7 \varphi \operatorname{sen} \varphi d \varphi=4^5 \int_1^{1 / 16}-\dfrac{1}{8} d u=
=-\left.128 u\right|_1 ^{1 / 16}=-(8-128)=120
Passo 8
Para a segunda, faremos:
\cos ^3 \varphi=v
-3 \operatorname{sen} \varphi \cos ^2 \varphi d \varphi=d v
\cos 0=1 \rightarrow v=1
\cos \pi / 4=\dfrac{\sqrt{2}}{2} \rightarrow v=\dfrac{\sqrt{2}}{4}
\int_0^{\frac{\pi}{4}} \cos ^2 \varphi \operatorname{sen} \varphi d \varphi=\int_1^{\frac{\sqrt{2}}{4}}-\dfrac{1}{3} d v=
=-\left.\dfrac{v}{3}\right|_1 ^{\sqrt{2} / 4}=-\dfrac{1}{3}\left(\dfrac{\sqrt{2}}{4}-1\right)=\dfrac{1}{3}-\dfrac{\sqrt{2}}{12}
Passo 9
Substituindo os valores, encontrados, temos:
\dfrac{2 \pi}{5}\left[120-\left(\dfrac{1}{3}-\dfrac{\sqrt{2}}{12}\right)\right]=
Resposta
\dfrac{718 \pi}{15}+\dfrac{\sqrt{2} \pi}{30}


