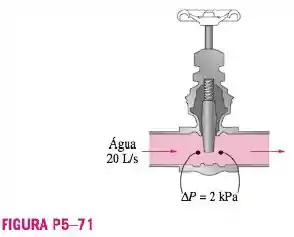
A água escoa a uma vazão de 20 L/s através de um tubo horizontal cujo diâmetro de uma válvula do tubo é medida como 2 kPa. Determine a perda de carga irreversível da válvula, e a potência de bombeamento útil necessária para superar a queda de pressão resultante.
Passo 1
Possuímos um tubo com um fluxo de água operando nele, uma válvula que produz uma queda de potencia neste fluxo. Temos que calcular a perda ou carga irreversível causada pela válvula e a potência de bombeamento necessária para superara queda.
Primeiramente temos que assumir que o fluxo é constante e incompressível, assumiremos também que o diâmetro do tubo é constante durante todo o processo.
Para lidarmos com esta válvula, tenha em mente que, temos parte de entrada, ou seja, todo fluxo que anda não passou pela válvula (1) e a parte de saída todo o fluxo que já passou pela válvula (2).
Perceba que ao assumirmos que fluxo é constante, incompressível temos que o fluxo de entrada é igual a fluxo de saída, também o diâmetro do tubo não varia, portanto, as velocidades V_1, de entrada e V_2, de saída serão iguais.
E por estamos analisando um tubo na horizontal, z_1=z_2.
Passo 2
Devido a estes fatos, do passo 1 , podemos escrever a equação do balanço energético:
\dfrac{P_1}{\rho g}+\alpha_1 \dfrac{V_1}{2 g}+z_1+h_{\text {bomba, } u t}=\dfrac{P_2}{\rho g}+\alpha_2 \dfrac{V_2^2}{2 g}+z_2+h_{\text {turbina }, e}+h_L
Temos a carga da bomba útil será igual à carga da turbina, devido fluxo constante, anulando as coordenadas z, \mathrm{e} as velocidades também:
\dfrac{P_1}{\rho g}=\dfrac{P_2}{\rho g}+h_L
Isolando a perda irreversível:
h_L=\dfrac{P_1-P_2}{\rho g}
Substituindo valores:
h_L=\dfrac{2 k\left[\dfrac{\mathrm{N}}{\mathrm{m}^2}\right]}{1000\left[\dfrac{\mathrm{kg}}{\mathrm{m}^3}\right] \bullet 9,81\left[\dfrac{\mathrm{m}}{\mathrm{s}^2}\right]}=0,2038 \mathrm{~m}
Passo 3
Para determinar a potência necessária para vencer a diferença de pressão da válvula pelo produto do fluxo pela ddp, tendo como:
Só vamos ficar atentos que nosso fluxo volumétrico se encontra na unidade de L / s, vamos converter para \mathrm{m}^3 / \mathrm{s}, unidade padrão:
Sabendo que 1 \mathrm{~m}^3=1000 \mathrm{~L}, fica:
\dot{V}=20\left[\frac{L}{s}\right] \cdot\left(\dfrac{1\left[m^3\right]}{1000[L]}\right)=0,02 \mathrm{~m}^3 / \mathrm{s}
Retomando ao cálculo de potência:
\dot{W}{\text {barmba }}=\dot{V} \bullet \Delta P \ \dot{W}{\text {bonka }}=0,02\left[\dfrac{m^3}{s}\right] \cdot 2 k[P a] \bullet\left(\dfrac{1[\mathrm{~W}]}{1\left[P a \bullet \dfrac{m^3}{s}\right]}\right)=40 \mathrm{~W}
Resposta
h_L = 0,2028 m
W_{bomba} = 40 W

