Uma parede de 4 m de altura e 6 m de largura consiste de tijolos horizontais com seção transversal de separados por camada de gesso de 3 cm de espessura. Existem ainda uma camadas de gesso 2 cm de espessura em cada lado da parede e uma espuma rígida de 2 cm de espessura sobre a face interna da parede. As temperaturas interna e externa são 22°C e -4°C, e os coeficientes de transferência de calor por convecção dos lados interno e externo são e , respectivamente. Assumindo a transferência de calor unidimensional e desconsiderando a radiação, determine a taxa de transferência de calor através da parede.
Passo 1
Muito bem galera, vamos pra mais uma!!
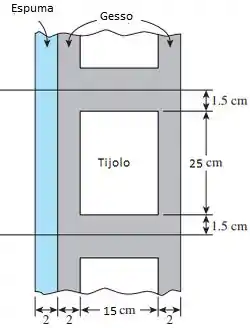
Antes de qualquer coisa nós vamos desenhar o que está acontecendo:

Legal, pelo esquema nós vemos que R_3, R_4 e R_5 estão em paralelo entre si, então:
\dfrac{1}{R_{345}}=\dfrac{1}{R_3}+\dfrac{1}{R_4}+\dfrac{1}{R_5}
Que está em sequência com as demais:
R_T=R_i+R_1+R_2+R_{345}+R_6+R_7
Até aqui tudo certo?
Passo 2
Agora vamos calcular cada resistência separadamente, ok?
R_i=\dfrac{1}{h_1 A}
R_1=\dfrac{L_{\text {espuma }}}{k_{\text {espuma }} A}
R_2=R_6=\dfrac{L_{\text {gesso }}}{k_{\text {gesso }} A}
R_3=R_5=\dfrac{L_{\text {gesso }}}{k_{\text {gesso }} A}
R_4=\dfrac{L_{\text {tijolo }}}{k_{\text {tijolo }} A}
R_7=\dfrac{1}{h_2 A}
O que fazemos então para achar a área? Vamos considera-lo unitário, ok?
w=1m
Relembrando os dados:
h_i=10 \dfrac{\mathrm{W}}{\mathrm{m}^2 \cdot \mathrm{K}}
k_{\text {espuma }}=0,026 \dfrac{\mathrm{W}}{\mathrm{m} \cdot \mathrm{K}}
L_{\text {espuma }}=2 \mathrm{~cm}=0,02 \mathrm{~m}
k_{\text {gesso }}=0,22 \dfrac{\mathrm{W}}{\mathrm{m} \cdot \mathrm{K}}
L_{\text {gesso.2 }}=L_{\text {gesso. }}=2 \mathrm{~cm}=0,02 \mathrm{~m}
L_{\text {gesso.4 }}=L_{\text {tijolo }}=15 \mathrm{~cm}=0,15 \mathrm{~m}
k_{\text {tijolo }}=0,72 \dfrac{\mathrm{W}}{\mathrm{m} \cdot \mathrm{K}}
h_7=20 \dfrac{\mathrm{W}}{\mathrm{m}^2 \cdot \mathrm{K}}
Bom galera, nós estamos considerando uma altura da parede referente a 28 cm, então:
R_i=\dfrac{1}{10 \dfrac{W}{m^2 \cdot K}(0,28 m \times 1 m)}=0,357 \dfrac{K}{W}
R_1=\dfrac{0,02 m}{0,026 \dfrac{W}{m \cdot K}(0,28 m \times 1 m)}=2,747 \dfrac{K}{W}
R_2=R_6=\dfrac{0,02 m}{0,22 \dfrac{W}{m \cdot K}(0,28 m \times 1 m)}=0,325 \dfrac{K}{W}
R_7=\dfrac{1}{20 \dfrac{W}{m^2 \cdot K}(0,28 m \times 1 m)}=0,179 \dfrac{K}{W}
Na resistências de número 3 e 5 a altura é equivalente à 1,5 cm, certo?
R_3=R_5=\dfrac{0,15 m}{0,22 \dfrac{W}{m \cdot K}(0,015 m \times 1 m)}=45,45 \frac{K}{W}
E para finalizar, a altura do tijolo equivale 25 cm:
R_4=\dfrac{0,15 m}{0,72 \dfrac{W}{m \cdot K}(0,25 m \times 1 m)}=0,83 \frac{K}{W}
E quanto a resistência total? Bora substituir, né?
Mas antes vamos calcular a resistência em paralelo:
\dfrac{1}{R_{345}}=\dfrac{1}{45,45 \dfrac{K}{W}}+\dfrac{1}{0,83 \dfrac{K}{W}}+\dfrac{1}{45,45 \dfrac{K}{W}}
\dfrac{1}{R_{345}}=1,249 \dfrac{W}{K}
Então:
R_{345}=0,8 \dfrac{K}{W}
Na resistência total:
R_T=0,357 \dfrac{K}{W}+2,747 \dfrac{K}{W}+0,325 \dfrac{K}{W}+0,8 \dfrac{K}{W}+0,325 \dfrac{K}{W}+0,179 \dfrac{K}{W}
R_T=4,733 \dfrac{K}{W}
Já achamos a resistência total, agora só precisamos do fluxo de calor!!
Passo 3
Se lembram de como calcular o calor?
Fácil, não é?
\dot{Q}=\dfrac{\Delta T}{R_T}
Substituindo:
\dot{Q}=\dfrac{22^{\circ} C-\left(-4^{\circ} C\right)}{4,733 \dfrac{K}{W}}
Como a variação em graus Celsius é a mesma que a variação em kelvin:
\dot{Q}=\dfrac{26 K}{4,733 \dfrac{K}{W}}
\dot{Q}=5,5 \mathrm{~W}
Como estamos analisando um espaço referente a 0,28 m de altura e 1 m de largura:
\dot{Q}=\dfrac{5,5 W}{0,28 m \times 1 m}=19,6 \dfrac{W}{m^2}
Como a cada intervalo de 0,28 m^2 a estrutura da parede se repete, para a parede total de 4 m de altura e 6 m de largura a troca total de calor será:
\dot{Q}=19,6 \dfrac{W}{m^2} \times(4 m \times 6 m)=470,4 W
Resposta
\dot{Q}=470,4 W

