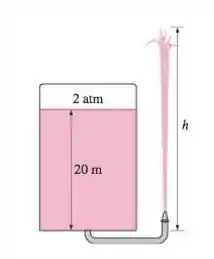
O nível da água em um tanque é de 20 m acima do solo. Uma mangueira está conectada à parte inferior do tanque, e o bocal no final da mangueira aponta diretamente para cima. A tampa do tanque é hermética e a pressão manométrica do ar acima da superfície da água é de 2 atm. O sistema está no nível do mar. Determine a altura máxima até a qual a corrente de água pode chegar.
Passo 1
Fala aí galera, bora pra mais uma questão de Mecânica dos Fluidos pra tirar aquele 10 na prova.
Primeiramente, pegamos o ponto (1) na superfície livre da água no tanque e o ponto (2) na parte superior da trajetória da água. Além disso, tomamos o nível de referência na parte inferior do tanque.
No topo da trajetória da água, V_2=0, e a pressão é igual a pressão atmosférica.
Observando que z_1=20 \mathrm{~m}, P_1=2 \mathrm{~atm}, P_2=P_{\text {atm }} e que a velocidade do fluido na superfície livre do tanque é muito baixa, podemos considerar V_1 \cong 0.
Passo 2
Com isso, podemos aplicar a equação de Bernoulli entre esses dois pontos, temos:
\dfrac{P_1}{\rho g}+\dfrac{V_1^2}{2 g}+z_1=\dfrac{P_2}{\rho g}+\dfrac{V_2^2}{2 g}+z_2 z_2=\dfrac{P_1-P_{\text {atm }}}{\rho g}+z_1=\dfrac{P_{1, \text { manométrica }}}{\rho g}+z_1
Sabemos que 2 a t m=202650 \mathrm{~N} / \mathrm{m}^2, logo:
z_2=\dfrac{202650 \mathrm{~N} / \mathrm{m}^2}{\left(1000 \dfrac{\mathrm{kg}}{\mathrm{m}^3}\right)\left(9,81 \dfrac{\mathrm{m}}{\mathrm{s}^2}\right)}+20 z_2=40,7 \mathrm{~m}
Resposta
z_2=40,7 m

